2008-08-01 [長年日記]
λ. 任天堂、複製したDSソフトを起動する「マジコン」販売業者を提訴
特許・著作権・商標の侵害とかではなく、不正競争防止法でのアクセスコントロールの迂回装置にあたるかが争点なのね。ちょっと意外な感じが……
2008-08-02 [長年日記]
λ. Categories with attributes (cwa)
依存型とcatamorphism の話を書くために、まずは依存型を持つ体系の圏論的なモデルとして Categories with attributes を導入する。
Categories with attributes
Category with attributes (cwa) は依存型を持つ計算体系の圏論的なモデルとしてよく使われる圏で、以下の構成要素と条件からなる。
- 圏 C
- 終対象 1∈|C|
- 前層 Fam : Cop → Set
- 射に対する作用については S[f] := Fam(f)(S) という記法を用いる。
- 任意の Γ∈|C| と S∈Fam(Γ) に対して、Γ・S ∈ |C| という対象と射 πS : Γ・S → Γ が存在する
- 記法を濫用して πS のことを、単に S と書くことがある。
- 任意の射 f : Δ → Γ と S∈Fam(Δ) に対して、射 f・S : Δ・S[f] → Γ・S が存在して、
![\xymatrix@+15pt{ \Delta\cdot S[f] \ar[r]^{f\cdot S} \ar[d]_{\pi_{S[f]}} & \Gamma\cdot S \ar[d]^{\pi_S} \\ \Delta \ar[r]_{f} & \Gamma }](tex/9872fd683cdeca608cfd2a568231f10c.png "\xymatrix@+15pt{ \Delta\cdot S[f] \ar[r]^{f\cdot S} \ar[d]_{\pi_{S[f]}} & \Gamma\cdot S \ar[d]^{\pi_S} \\ \Delta \ar[r]_{f} & \Gamma }")
がpullbackになっていて、さらに idΓ・S = idΓ・S と (f∘g)・S = (f・S)∘(g・S[f]) が成り立つ
依存型を持つ体系のcwaでの大雑把な解釈
まず、πS の section からなる集合を Tm(Γ, S) := {M: Γ→Γ・S | πS∘M = idΓ} と書くことにする。 そうすると、依存型を持つ体系はcwaに大雑把にはこんな感じで対応する。
- 文脈 Γ は Γ∈|C| に対応し
- 文脈 Γ での型 S 、すなわち Γ ├ S set であるような S は、S∈Fam(Γ) に対応
- 文脈 Γ での項 M 、すなわち Γ ├ M : S であるような M は、M∈Tm(Γ, S) に対応
これは一見すると奇妙な解釈に見えるけど、スライス C/Γ を考えると、普通の解釈を一般化したものになっている。
C/Γでの終対象は C の idΓ: Γ→Γ なので、C での πS : Γ・S → Γ を C/Γ では単にSと書くことにすると、M∈Tm(Γ, S) は C/Γ ではちゃんと点 1→S とみなすことが出来る。
![\xymatrix{ \Gamma \ar@{=}[dr] \ar[rr]^{M} & & \Gamma\cdot S \ar[dl]^{\pi_S} \\ & \Gamma }](tex/9290b2e4239bb1d1a496f2e193a437df.png "\xymatrix{ \Gamma \ar@{=}[dr] \ar[rr]^{M} & & \Gamma\cdot S \ar[dl]^{\pi_S} \\ & \Gamma }")
代入
それから、M∈Tm(Γ, S) と f : Δ→Γ に対して、M[f] ∈ Tm(Δ, S[f]) を、pullback の性質から以下の図のように定義する。
![\xymatrix@+15pt{ \Delta \ar@{=}@/_1pc/[ddr] \ar@/^1pc/[rrd]^{M\circ f} \ar@{.>}[dr]|{M[f]} \\ & \Delta\cdot S[f] \ar[r]_{f\cdot S} \ar[d]^{\pi_{S[f]}} & \Gamma\cdot S \ar[d]^{\pi_S} \\ & \Delta \ar[r]_{f} & \Gamma }](tex/bc33472fef904aae3e1c932788a73fed.png "\xymatrix@+15pt{ \Delta \ar@{=}@/_1pc/[ddr] \ar@/^1pc/[rrd]^{M\circ f} \ar@{.>}[dr]|{M[f]} \\ & \Delta\cdot S[f] \ar[r]_{f\cdot S} \ar[d]^{\pi_{S[f]}} & \Gamma\cdot S \ar[d]^{\pi_S} \\ & \Delta \ar[r]_{f} & \Gamma }")
S[f] や M[f] と書いたが、これらはもちろん代入(substitution)を表している。
例えば、Γ ├ N : T と Γ, x : T ├ M : S から Γ ├ M[x:=N] : S[x:=N] を得ることが、N ∈ Tm(Γ, T) と M ∈ Tm(Γ・T, S) から M[N] ∈ Tm(Γ, S[N]) を得ることに対応している。
![\xymatrix@+15pt{ \Gamma\cdot S[N] \ar[d]^{\pi_{S[N]}} \ar[r]^{N\cdot S} & \Gamma\cdot T\cdot S \ar[d]^{\pi_S} \\ \Gamma \ar[r]_{N} \ar@<1ex>[u]^{M[N]} & \Gamma\cdot T \ar@<1ex>[u]^{M} }](tex/3b0d4e5438f5326eead985369047b0ea.png "\xymatrix@+15pt{ \Gamma\cdot S[N] \ar[d]^{\pi_{S[N]}} \ar[r]^{N\cdot S} & \Gamma\cdot T\cdot S \ar[d]^{\pi_S} \\ \Gamma \ar[r]_{N} \ar@<1ex>[u]^{M[N]} & \Gamma\cdot T \ar@<1ex>[u]^{M} }")
このように、構文的な代入を意味論的な代入にうまく対応させられるのが、cwaの嬉しいところ。
ただ、ちょっと面倒なのは weakening をする際にも、型や項の側では要らない変数を捨てるような代入を明示的に適用しなくてはいけないところ。
例えば、Γ ├ S set と Γ ├ M : S から weakening で Γ, x : T ├ S set と Γ, x : T ├ M : S を得るのは、S∈Fam(Γ) と M∈Tm(Γ, S) から、πT : Γ・T → Γ を使って S[πT]∈Fam(Γ・T) と M[πT]∈Tm(Γ・T, S[πT]) を得ることに対応する。
![\xymatrix@+15pt{ \Gamma\cdot T\cdot S[\pi_T] \ar[d]^{\pi_{S[\pi_T]}} \ar[r]^{\pi_T\cdot S} & \Gamma\cdot S \ar[d]^{\pi_S} \\ \Gamma\cdot T \ar[r]_{\pi_T} \ar@<1ex>[u]^{M[\pi_T]} & \Gamma \ar@<1ex>[u]^{M} }](tex/134a576fd7c64d1e5c6a58cf99e0eb54.png "\xymatrix@+15pt{ \Gamma\cdot T\cdot S[\pi_T] \ar[d]^{\pi_{S[\pi_T]}} \ar[r]^{\pi_T\cdot S} & \Gamma\cdot S \ar[d]^{\pi_S} \\ \Gamma\cdot T \ar[r]_{\pi_T} \ar@<1ex>[u]^{M[\pi_T]} & \Gamma \ar@<1ex>[u]^{M} }")
これくらいの例なら問題ないのだけど、ちょっと複雑なものを書こうとすると、すぐ訳がわかんなくなってしまうよ……*1
*1 うまい絵算の方法でもあるといいんだけどねぇ
2008-08-04 [長年日記]
λ. cwaでのユニット型の解釈
Categories with attributes (cwa) で cwa の簡単な説明を書いたので、今度は cwa で幾つかの基本的な型を扱ってみることに。 まずは一番簡単と思われるユニット型を。
構成規則と導入規則
通常扱う構成規則と導入規則は以下のような形になっている。
--------------- Γ ├ Unit set Γ ├ () : Unit
これだと任意のΓについて考えなければならず面倒くさいが、実際のところはそれらの解釈はΓが空である場合からweakeningによって得たものと等しくなければならないので、Γを空の場合に限定した以下の規則を考えることにする。
-------------- ├ Unit set ├ () : Unit
これはそれぞれ Unit ∈ Fam(1) と () ∈ Tm(1, Unit) で解釈される。 Γが空でない場合は、weakening -[!Γ] を使って Unit[!Γ]∈Fam(Γ) と ()[!Γ]∈Tm(Γ, Unit[!Γ]) で解釈できる。
除去規則
お次は除去規則で、通常の除去規則はこんな形をしている。
Γ, x : Unit ├ P set Γ ├ M : P[x:=()] Γ ├ N : Unit -------------------------------- Γ ├ elim(P,M,N) : P[x:=N] Γ ├ elim(P,M,())=M : P[x:=()]
ただ、これも少し扱いにくいので、少し変えて、以下のような規則を考える。
Γ, x : Unit ├ P[x] set Γ ├ M : P[()] --------------------------------------------- Γ, x : Unit ├ elim(P,M)[x] : P[x] Γ ├ elim(P,M0)[()] = M : P[()]
これの解釈は、 任意の P ∈ Fam(Γ・Unit[!Γ]) と M ∈ Tm(Γ, P[()[!Γ]]) に対して、 elim(C,M) ∈ Tm(Γ・Unit[!Γ], P) が存在し、 elim(C,M)[()[!Γ]] = M ∈ Tm(Γ, P[()[!Γ]]) が成り立つということになる。 図で書くと以下のような感じになる。
![\xymatrix@+15pt{ \Gamma \ar[r]^{() [!_\Gamma]} \ar@{.>}[d]|{\mathrm{elim}(C,M)[() [!_\Gamma]]=M} & \Gamma\bullet \mathrm{Unit}[!_\Gamma] \ar@{.>}[d]|{\mathrm{elim}(C,M)} \\ \Gamma\bullet P[() [!_\Gamma]] \ar[r]_{() [!_\Gamma]\bullet P} & \Gamma\bullet\mathrm{Unit}[!_\Gamma]\bullet P }](tex/01fb9550331c65c1e82609c42fb49928.png "\xymatrix@+15pt{ \Gamma \ar[r]^{() [!_\Gamma]} \ar@{.>}[d]|{\mathrm{elim}(C,M)[() [!_\Gamma]]=M} & \Gamma\bullet \mathrm{Unit}[!_\Gamma] \ar@{.>}[d]|{\mathrm{elim}(C,M)} \\ \Gamma\bullet P[() [!_\Gamma]] \ar[r]_{() [!_\Gamma]\bullet P} & \Gamma\bullet\mathrm{Unit}[!_\Gamma]\bullet P }")
2008-08-05 [長年日記]
λ. Categories with families
Categories with attributes を使って色々書こうとしてたけど、Categories with attributes とは別に Categories with families というのがあって、こっちの方が扱いやすいようだ。しょぼーん。
一応、定義とかをメモしておく。
圏 Fam(C)
- 対象 A=(A0, A1)
- 集合 A0 と A0 によって添え字付けられたCの対象の族 {A1a}a∈A0 の組
- 射 f=(f0,f1) : A→B
- 関数 f0 : A0 → B0 と、Cの射の族 {f1a : A1a → B1f0(a)}a∈A0 の組
ちなみに、Fam(C)から第一成分を射影する関手 Fam(C)→Set は、Bart Jacobs の Categorical Type Theory で「"Family fibration" Fam(C)→Sets」と呼ばれているもの。
comprehension
関手 F=(Ty,Tm) : Cop→Fam(Set) と Γ∈|C| と σ=Ty(Γ) が与えられているとする。 σ の comprehension は以下の構成要素と条件からなる。
- Γ・σ ∈ |C| と
- p(σ) : Γ・σ → Γ
- vσ : Tm(Γ・σ, σ[p(σ)])
- 任意の f : Δ→Γ と M∈Tm(σ[f]) 対して、p(σ)∘<f,M>σ = f かつ vσ[<f,M>σ] = M であるような射 <f,M>σ : Δ → Γ・σ が一意に存在。
Categories with families
Categories with families (CwF) は以下の構成要素と条件からなる。
- 圏 C
- 終対象 1∈|C|
- 関手 F=(Ty,Tm) : Cop→Fam(Set)
- Γ∈|C| と σ∈Ty(Γ) に対して comprehension が存在
Categories with Attributes との関係
.
2008-08-06 [長年日記]
λ. Audible で Getting Things Done の原典を
20080623#p01 にダウンロードした God's Equation はとっくに聴き終わっていて、7月分のクレジットで何を買おうかしばらく悩んでいた。 で、今日Audibleのサイトを適当に眺めていたら、たまたまGetting Things Done: The Art of Stress-Free Productivity を見かけてたので、「そういえばこれまで原典は読んだことがなかったな」と思って購入してみた。まだ聴いてないけど、David Allen 本人が読んでるのね。
2008-08-07 [長年日記]
λ. セゾン・バンガード・グローバルバランスファンド
月曜に セゾン・バンガード・グローバルバランスファンド の資料請求をしたら、もう届いた。 早いなぁ。
2008-08-08 [長年日記]
λ. マネックス証券の口座開設キャンペーン
マネックス証券が 新規口座開設 & 5万円以上(MRF買い付け)入金で、Amazon®ギフト券5,000円分プレゼント！ というキャンペーンをやっていた。 マネックス証券は、夜間取引のマネックスナイターとか幾つか気になっている機能があって、いい機会なので申し込んでみた。
λ. オリンピック開会式
演出過剰だけど、流石中国はスケールが大きいなと思わせる内容だった。 北朝鮮のマスゲームなんて目じゃないな。 まあ、飽きて途中で見るのを止めてしまったけど。
ところで、エクストリーム・聖火リレーの表彰式 ﾏﾀﾞｧ-? （･∀･ ）っ/凵⌒☆ﾁﾝﾁﾝ
2008-08-09 [長年日記]
λ. 首を捻った
朝、腹筋を終えて起き上がるときに首を捻ってしまった。その後、近くのプールに行き、また1kmを30分くらいで泳いできた。首が気になって、ちょっと泳ぎにくかったがあまり気にはならなかった。お昼を食べて、午後はRHG読書会へ。そこで下を向いて本を読む際に首がしばしば酷く痛むことに気づく。これはこれまで寝違えたりした中で最悪かもしれない。しんどい……。一晩寝て直らなかったら病院へ行こっと。
λ. RHG読書会::東京 Practical Common Lisp 第九回
ついに出版された 実践Common Lisp(Peter Seibel/佐野匡俊/水丸淳/園城雅之/金子祐介) の第19章「例外処理を超えて : コンディションと再起動」、第20章「特殊オペレータ」、第21章「大規模開発に向けて : パッケージとシンボル」。
第19章「例外処理を超えて : コンディションと再起動」は非常に面白そうな話だったが、遅れていったために聞き逃してしまった。 第21章「大規模開発に向けて : パッケージとシンボル」では、Lispのシンボルのinternとかuninternといった概念について初めて理解でき、「流石にLispは良く考えられているなぁ」と感動した。
二次会では青島ビールを飲みながら、オリンピック談義などを。
![[青島ビール]](./images/20080809_0.jpg)
λ. ガラスでもやしもんの菌を
ガラス細工でもやしもんの菌を作る動画をみて感動した。
2008-08-10 [長年日記]
λ. 首の痛み
湿布をはって一晩寝たら、首の痛みはだいぶ良くなって、普通の寝違えくらいになった。ので、とりあえず病院へは行かないことに。良かった、良かった。でも、色々疲れていたのか、目が覚めたのはもうお昼ごろだった。午後は圏論勉強会へ。
λ. 第四十三回圏論勉強会
Abramskyの"Temperley-Lieb algebra: From knot theory to logic and computation via quantum mechanics"の3回目で、今回は 4 Factorization and Idempotents と、5 Categorical Quantum Mechanics の 5.1 Outline of the approach まで。
私は遅れていったので、4 Factorization and Idempotents のところは聞き逃してしまった。(後で書く)
![[〈π||ψ〉の図]](./images/20080810_2.png)
5 Categorical Quantum Mechanics は記法が紛らわくて、少し混乱してしまった。▽がstateでbra、△がcostateでket。
特に混乱させられたのが「we also need to consider diamonds which arise by post-composing a state with a matching costate」という部分で、postが意味的な「後」なのか π∘ψ と書いた時の構文的な「後」なのかと、どっちにどっちをくっつけるのかが……(涙
今回の個人的な収穫は、Bob Coecke の Introducing categories to the practicing physicist (c.f. ヒビルテ(2007-05-15))への理解を深められたこと。
- 一つ目は、ベル状態 1 ↦ |0〉 ⊗ |0〉 + |1〉 ⊗ |1〉 のような書き方の意味が分かり、その性質もちょっと分かったこと。といっても、こないだ20080630#p01で読んだQMLの話で、有限次元のヒルベルト空間についてちょっとだけ理解出来ていたのを、再確認したという感じだけど。
- 二つ目は、最後の量子テレポーテーションの図が物理的にどんな現象を表しているのかを知ることが出来たこと。
![[量子テレポーテーションの図]](./images/20080810_0.png)
それと、Christopher Isham という人がコンパクト閉圏のような圏ではなくトポスを使おうとしているという話を教えてもらった。
二次会はお好み焼き。
![[ぼてぢゅうのお好み焼き]](./images/20080810_1.jpg)
2008-08-11 [長年日記]
λ. 『やっぱりあぶない、投資信託—あなたの「虎の子」の増やし方・使い方』 by 水沢 溪
最近、投資信託についての本を何冊か借りて読んでいるのだけど、そのなかで「これは酷い」と思った本。
変なところは色々あるけど、例えばp.103の「国債よりも大企業の社債の方が安全」というのは明らかに変。さらに、国がいつデフォルトしても不思議ではなく、破綻したら猛烈なインフレが起こるいうことを書いてるんだけど、それなのに円建ての債権を勧めるというのは、自己矛盾してるとしか思えない。
あと、p.56では「わかっている人がもし投資を考えるなら、直接株式とか不動産投資を選ぶでしょう」と書いているけど、p.109でのわかっている人向けの直接株式を勧めでは「日経新聞が楽観的な記事を載せなくなったころに『これぞ』と思う株を3分の1だけ買ってみてください。あとはあなたの勘が働きますよ」とあって、「勘かよ…」と呆れた。
投信は証券会社にとって「裏活用」出来ておいしいという辺りの話は面白かったが、全体的に投信への不安を煽るだけで他の投資先との公平な比較はなされておらず、また資産運用のアドバイスは原理原則に基づいたものというよりも単に著者の感覚的なものでしかないので、真面目な資産運用の検討には全く役に立たない。
λ. 雑記
公私共に色々と失敗してしまって、非常に憂鬱。
2008-08-12 [長年日記]
λ. cwaでの自然数型の解釈
(書きかけ)
この間はユニット型について考えたので、今度は自然数型を。
自然数型の規則
自然数型に関する通常の規則は以下のようなもの。
--------------
Γ ├ N : set
Γ ├ 0 : N
Γ ├ M : N
--------------
Γ ├ s(M) : N
Γ, n : N ├ C set
Γ ├ M0 : C[n:=0]
Γ, n : N, x : C ├ Ms : C[n:=s(n)]
Γ ├ M : N
--------------------------------------
Γ ├ elim([n]C,M0,Ms,M) : C[n:=M]
Γ ├ elim([n]C,M0,Ms,0) = M0 : C[n:=0]
Γ ├ elim([n]C,M0,Ms,s(M)) =
Ms[n:=M, x:=elim([n]C,M0,Ms,M)] : C[n:=s(M)]
なんだけど、例によって以下のように変形した規則で考える。
---------
├ N set
├ 0 : N
---------------
x:N ├ s[x] : N
Γ, x:N ├ P[x] set
Γ ├ M0 : P[0]
Γ, x:N, y:P[x] ├ Ms[x,y] : P[s[x]]
------------------------------------
Γ, x:N ├ elim(P,M0,Ms)[x] : P[x]
Γ ├ elim(P,M0,Ms)[0] = M0 : P[0]
Γ, x:N ├ elim(P,M0,Ms)[s[x]]
= Ms[x, elim(P,M0,Ms)[x]] : P[s[x]]
省略記法
cwaでの解釈をまともに書いていると大変なので、ちょっと略記法を導入する。(後で書く)
cwaでの解釈
で、cwaで解釈するとこうなる。
- N∈Fam(1)
- 0∈Tm(1, N)
- s∈Tm(1・N, N+)
- P∈Fam(Γ・N+), M0∈Tm(Γ, P[0+]), Ms∈Tm(Γ・N+・P, P[π・N+][s+][π]) が与えられたとき、h=elim(P,M0,Ms)∈Tm(Γ・N+, P) が存在し、h[0+]=M0, h[π・N+][s+]=Ms[h] が成り立つ。
![\xymatrix@+20pt{ \Gamma \ar[r]^{0^{+}} \ar[d]|{h[0^{+}]=M_0} & \Gamma\cdot N^{+} \ar[d]^h \\ \Gamma\cdot P[0^{+}] \ar[r]_{0^{+}\cdot P} & \Gamma\cdot N^{+}\cdot P }](tex/3f9b7cee876ecac53c8b09df323baa05.png "\xymatrix@+20pt{ \Gamma \ar[r]^{0^{+}} \ar[d]|{h[0^{+}]=M_0} & \Gamma\cdot N^{+} \ar[d]^h \\ \Gamma\cdot P[0^{+}] \ar[r]_{0^{+}\cdot P} & \Gamma\cdot N^{+}\cdot P }")
![\xymatrix@+20pt{ \Gamma\cdot N^{+} \ar[rr]^{s^{+}} \ar[d]|{h[\pi\cdot N^{+}][s^{+}]=M_s[h]} & & \Gamma\cdot N^{+}\cdot N^{+} \ar[d]|{h[\pi\cdot N^{+}]} \ar[r]^{\pi\cdot N^{+}} & \Gamma\cdot N^{+} \ar[d]^{h} \\ \Gamma\cdot N^{+}\cdot P[\pi\cdot N^{+}][s^{+}] \ar[rr]_{s^{+}\cdot P[\pi\cdot N^{+}]} & & \Gamma\cdot N^{+}\cdot N^{+}\cdot P[\pi\cdot N^{+}] \ar[r]_-{\pi\cdot N^{+}\cdot P} & \Gamma\cdot N^{+}\cdot P }](tex/8babf88d37750599ce5d3ae3009d101c.png "\xymatrix@+20pt{ \Gamma\cdot N^{+} \ar[rr]^{s^{+}} \ar[d]|{h[\pi\cdot N^{+}][s^{+}]=M_s[h]} & & \Gamma\cdot N^{+}\cdot N^{+} \ar[d]|{h[\pi\cdot N^{+}]} \ar[r]^{\pi\cdot N^{+}} & \Gamma\cdot N^{+} \ar[d]^{h} \\ \Gamma\cdot N^{+}\cdot P[\pi\cdot N^{+}][s^{+}] \ar[rr]_{s^{+}\cdot P[\pi\cdot N^{+}]} & & \Gamma\cdot N^{+}\cdot N^{+}\cdot P[\pi\cdot N^{+}] \ar[r]_-{\pi\cdot N^{+}\cdot P} & \Gamma\cdot N^{+}\cdot P }")
![\xymatrix@+20pt{ \Gamma\cdot N^{+} \ar[d]_{M_s[h]} \ar[rr]^h & & \Gamma\cdot N^{+}\cdot P \ar[d]^{M_s} \\ \Gamma\cdot N^{+}\cdot P[\pi\cdot N^{+}][s^{+}] \ar[rr]_-{h\cdot P[\pi\cdot N^{+}][s^{+}][\pi]} & & \Gamma\cdot N^{+}\cdot P\cdot P[\pi\cdot N^{+}][s^{+}][\pi] }](tex/49e9f9dc8ea37c97bde41a957570c4e3.png "\xymatrix@+20pt{ \Gamma\cdot N^{+} \ar[d]_{M_s[h]} \ar[rr]^h & & \Gamma\cdot N^{+}\cdot P \ar[d]^{M_s} \\ \Gamma\cdot N^{+}\cdot P[\pi\cdot N^{+}][s^{+}] \ar[rr]_-{h\cdot P[\pi\cdot N^{+}][s^{+}][\pi]} & & \Gamma\cdot N^{+}\cdot P\cdot P[\pi\cdot N^{+}][s^{+}][\pi] }")
λ. お菓子買いだめ
今月は少なめで。
![[お菓子]](./images/20080812_0.jpg)
2008-08-13 [長年日記]
λ. 箱根 彫刻の森美術館
箱根 彫刻の森美術館 に行ってきた。奇怪なオブジェが沢山あって楽しい。昔、子供のころにも行ったことがあるはずなのだけど、それはあまり覚えてなくて、むしろ「これ美術の教科書でみたことあるな」という方が多かった。有名な作品は置いておくとして、個人的に少し印象に残ったのは、峯孝の1972のプリマヴェラ(Primavera)という作品。それから、足湯につかってきた。
2008-08-14 [長年日記]
今日も1kmを30分くらいで泳いできた。
λ. スカイ・クロラ The Sky Crawlers
映画の「スカイ・クロラ The Sky Crawlers」を観て来た。 森博嗣の原作は昔読んだけど、内容はすっかり忘れてた。原作を読んだときは、なんだか肌に合わない気がして続編も読んでいなかったのだけど、また読み返したてみるかなぁ。 あと、推進式(プッシャ)の戦闘機が飛んでる映像*1なんて見たの初めてだったので、ちょっと感動。
*1 アニメだけど
λ. 「量子の世界の情報工学 —可能性の波を求めて—」
量子テレポーテーションに関して調べものをしていて、たまたま検索に引っかかった「量子の世界の情報工学 —可能性の波を求めて—」というのを読んだ。
2008-08-15 [長年日記]
特に何もせずすごす。
λ. The Comonad.Reader » Kan Extensions
活動記録/20080529 - ocaml-nagoya の次回予告に載っていた The Comonad.Reader » Kan Extensions を読んだ。
Haskellを使って説明すると、登場するのがHaskellの型と関数からなる圏だけで、複数の圏が登場しなくなってしまうので、極限や余極限の説明等ちょっと苦しい感じがする部分もある。けど、面白い。Kan拡張の定義を知ってはいたけど、これを読んで少し慣れることが出来た。
あと、category-extrasって昔 Category extras - ヒビルテ (2004-12-09) で取り上げたときから、ずいぶん色々追加されているのね。
関連
2008-08-16 [長年日記]
今日も1kmを30分くらいで泳いできた。 その後、某映画館にダークナイトを観に行ったら、時間を間違えていたので、何も観ずに帰ってきてしまった。それから、読みかけのまま放置していた Decoding the Universe: How the New Science of Information Is Explaining Everything in the Cosmos, fromOur Brains to Black Holes(Charles Seife) を読み終える。
2008-08-17 [長年日記]
連休終わり
![[靖国神社]](./images/20080817_0.jpg)
朝起きたら、空気がひんやりしていて驚いた。いきなり秋めいてきた感じ。今日は泳ぎにいくのは諦める。その代わり、靖國神社に参拝して遊就館を見学しに行く。その帰りに映画「崖の上のポニョ」を見てきた。
そういえば、今年はコミケには行かなかったな。
2008-08-18 [長年日記]
λ. 自然変換の垂直合成と水平合成
こないだまで圏論勉強会で読んでいた「The Haskell Programmer's Guide to the IO Monad — Don't Panic」を ocaml-nagoya でも読んでいたようだ。 それで、活動記録/20080501 - ocaml-nagoya に自然変換の合成に関して「どこがverticalなのかよくわかりませんでした」と書いてあるのを見かけたので、ちょっと補足。
どこがverticalかというと、このテキストには出てこないけど、自然変換にはもう一つ「水平」合成があるからで、図式の描き方の慣例から「垂直合成(vertical composition)」「水平合成(horizontal composition)」と呼ばれている。
まず、以下の図のように縦に積まれた自然変換 τ と σ を合成するのが垂直合成 τ・σ : F → H で、(τ・σ)X := τX ∘ σX で定義される。
![\UseAllTwocells\xymatrix@+20pt{ C \ruppertwocell^F{\sigma} \ar[r]|{G} \rlowertwocell_H{\tau} & D }](tex/4707f7b36ea4543701f599af365b0924.png "\UseAllTwocells\xymatrix@+20pt{ C \ruppertwocell^F{\sigma} \ar[r]|{G} \rlowertwocell_H{\tau} & D }")
次に、以下の図のように横に並べられた自然変換 τ と σ を合成するのが水平合成 τ ∘ σ : F'F → G'G で、τG・F'σ = G'σ・τF で定義される。
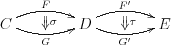
定義の図:
![\xymatrix{F'F \ar[r]^{F'\sigma} \ar[d]_{\tau F} & F'G \ar[d]^{\tau G} \\ G'F \ar[r]_{G'\sigma} & G'G }](tex/cbc8df47312af219b508a5d3b8323c07.png "\xymatrix{F'F \ar[r]^{F'\sigma} \ar[d]_{\tau F} & F'G \ar[d]^{\tau G} \\ G'F \ar[r]_{G'\sigma} & G'G }")
ここまで書いてから気づいたけど、圏論勉強会のときも同じような図を描いてた。このときの図では、水平合成の方に黒丸「・」を使ってしまっているので、その部分はちょっと違うけど。
何故違ってしまっているかというと、合成が二つもあると射の合成と同じ記法(「τ∘σ」や「τσ」)をどちらに使うかはちょっと悩ましいんだよね。 通常は水平合成に射の合成と同じ記号を使っていて、これは2-圏とか色々な観点からは都合が良いのだけど、一方でHaskellから自然変換≒多相関数という対応で理解する場合には、垂直合成に対して関数合成の記号を使いたくもあって、このときは後者の考えで図を描いたんだろう(多分)。
2008-08-19 [長年日記]
λ. QMLで量子テレポーテーション
先日の圏論勉強会での量子テレポーテーションの話について、みんな色々書いているようだ。
参考:
- ベル状態、少し分かった、がやっぱりよくは分からん - 檜山正幸のキマイラ飼育記
- ベル状態について。 - hiroki_fの日記
- 勉強会その後：量子テレポーテーション - たけをの日記＠天竺から帰ってきたよ
私もご多分にもれず悩んでいて、それで、ふと「プログラミング言語で書いてみたら分かり易くなるんじゃ」と思ってQML(c.f. 20080630#p01)で書こうとしたら、コンパイラのサンプルとして既に用意されていた。teleport.qml
記法
記法は論文「A functional quantum programming language」のときには
Qnot : qb -o qb Qnot x = ifo x then qfalse else qtrue
だったのが、
Qnot (b,qb) |- ifo b then qfalse else qtrue :: qb;
という形式に変更になっている。 判定(judgement)そのものに名前をつけた感じか。 ただ、文脈部分では (変数, 型) よりも (変数 :: 型) と書けるといいのにと思った。
ここで、ifo は観測を伴わないを伴わない分岐で、then式とelse式がstrictな項*1でかつ直交している必要がある。ifoを使うと、制御NotやEPRペアの生成は以下のように定義できる。
-- A quantum CNOT operation
CNot (s,qb) (t,qb) |- ifo s then (qtrue,Qnot (t))
else (qfalse,t) :: qb*qb;
-- The constant EPR pair
Epr |- hF * (qtrue,qtrue) + hF * (qfalse,qfalse) :: qb*qb;
また、普通の if もあって、こちらは条件が不要で、代わりに decoherence を引き起こすようになっている。これを使うとqubitに対する観測は以下のように定義できる。
-- The measurement operator, using "if" Meas (x,qb) |- if x then qtrue else qfalse :: qb;
ifやcaseが観測に対応するというのは、遅延評価を行う関数型言語を使ったことがある人にとっては馴染み深いのではないかと思う。それらの言語でも、遅延評価されたサンクはある意味では値が確定していない状態であって、それに対してifやcaseによる分岐を適用することで評価が駆動されて値が確定するので。もちろん普通の関数型言語のサンクは干渉したりはしないけど。
teleport.qml
で、このteleport.qmlを読むと、量子テレポーテーションはまさに、たけをさんの日記に貼ってあった以下の図そのものなのね。
![[量子テレポーテーションの図]](./images/20080819_0.gif)
図の |00〉 + |11〉 の部分に相当するのが上で定義した Epr 。 そして、図の MBell に相当する以下の Bmeas では (Had ⊗ id)∘CNot を適用した結果に観測を行って 2bit の古典情報を得ている。QMLには古典情報用のデータ型といったものは特に用意されていないので、データ型としては qb*qb のままだけど。
-- The Bell-measurement operation
Bmeas (x,qb) (y,qb) |- let (xa,ya) = CNot (x,y)
in (Meas (Had (xa)),Meas (ya)) :: qb*qb;
Bnmeas (x,qb) (y,qb) |- let (xa,ya) = CNot (x,y)
in (Had (xa),ya) :: qb*qb;
そして、量子テレポーテーションの過程全体を表したのが、以下の Tele で、U では 2bit の古典情報をもとに4つのユニタリー変換のどれかを適用して、もとの状態を復元している。
Tele (a,qb) |- let (b,c) = Epr ()
in let f = Bnmeas (a,b)
in U (c,f) :: qb;
Bmeas ではなく、観測を伴わない Bnmeas の方を用いているのは何故か結構悩んでしまったのだけど、たけをさんと話したら「U内部のifでdecoherenceは起こるのでプログラム的には変わらないから」ということのよう*2。
2008-08-22 [長年日記]
λ. The principle of deferred measurement
QMLで量子テレポーテーションで、Bmeasの代わりに観測を行わないBnmeasを使っている理由について、「『U内部のifでdecoherenceは起こるのでプログラム的には変わらないから』ということのよう」と書いたが、実際には観測はいくらでも先延ばし可能なようだ。
QML の Jonathan Grattage の博士論文 QML: A functional quantum programming language に、Quantum Computation and Quantum Information (Cambridge Series on Information and the Natural Sciences)(Michael A. Nielsen/Isaac L. Chuang)*1からの引用があったので、孫引きしてみる。
Measurements can always be moved from an intermediate stage of a quantum circuit to the end of the circuit; if the measurement results are used at any stage of the circuit then the classically controlled operations can be replaced by conditional quantum operations.
2008-08-23 [長年日記]
λ. QMLから量子回路へのコンパイル
QMLで量子テレポーテーションの続きで、QMLのプログラムを実際にコンパイルして遊んでみる。出力先は色々選べるが、とりあえず型付きの量子回路へのコンパイルを試してみることに。qml.hsをghciで読み込んで、runTC "ファイル名" "識別子" とすれば、型付きの量子回路へと変換される。
Qnot
-- The quantum Not operation (Pauli X) Qnot (b,qb) |- ifo b then qfalse else qtrue :: qb;
まずはこのQnotをコンパイルしてみる。
Prelude QML> runTC "teleport.qml" "Qnot"
OK (TCirc {inT = {Q2}, outT = Q1 :<*> Q2, hpS = 0, gbS = 0, circ = Not})
inT が入力の「文脈」を表していて、outTは出力の「型」を表している。ただ、単なる Q2 ではなく Q1⊗Q2 になっているのは何でなんだろう。Q1⊗Q2 ≅ Q2 なので、構わないといえば構わないのだけど。
それから、hpS = 0 はヒープのサイズが 0 qubit で inT 以外の余計な領域を必要としないことを、gbS = 0 はゴミのサイズが 0 qubit で余計なゴミが出力されないことを表している。circ が回路本体で、ここでは単純なNotゲートになっている。
アダマール変換
-- The Hadamard operation
Had (b,qb) |- ifo b then hF * qfalse + (-hF) * qtrue
else hF * qfalse + hF * qtrue :: qb;
次にアダマール変換 Had の場合には「TCirc {inT = {Q2}, outT = Q1 :<*> Q2, hpS = 0, gbS = 0, circ = Seq (Rot (0.7071067811865475 :+ 0.0,0.7071067811865475 :+ 0.0) ((-0.7071067811865475) :+ -0.0,0.7071067811865475 :+ 0.0)) (Not)}」が得られる。
ここで、Rot (λ0, λ1) (κ0, κ1) は以下で定義されるユニタリー変換を表しているようだ。
- qfalse ↦ λ0 qfalse + λ1 qtrue
- qtrue ↦ κ0 qfalse + κ1 qtrue
これを行列で表すと ![\[\left( \begin{array}{rr} \lambda_0 & \kappa_0 \\ \lambda_1 & \kappa_1 \end{array} \right)\]](tex/5b5eb59120a323fedf0d9d74f7266cf1.png "\[\left( \begin{array}{rr} \lambda_0 & \kappa_0 \\ \lambda_1 & \kappa_1 \end{array} \right)\]")
になる。
Had の出力に現れる Rot の場合には、![\[\frac{1}{\sqrt{2}} \left( \begin{array}{rr} 1 & -1 \\ 1 & 1 \end{array} \right) = \left( \begin{array}{rr} 0.7 & -0.7 \\ 0.7 & 0.7 \end{array} \right)\]](tex/42d7b7eef0e40a5380949be3692064b3.png "\[\frac{1}{\sqrt{2}} \left( \begin{array}{rr} 1 & -1 \\ 1 & 1 \end{array} \right) = \left( \begin{array}{rr} 0.7 & -0.7 \\ 0.7 & 0.7 \end{array} \right)\]")
という行列を表している。
そして、Seq φ ψ は ψ ∘ φ という合成を表しているようだ。
Not も内部的には Rot (0,1) (1,0) で表現されているので、行列で表して計算してみると、通常のアダマール変換(Hadamard transform)になっているのが確認できる。
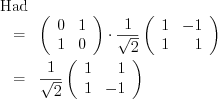
EPR
-- The constant EPR pair Epr |- hF * (qtrue,qtrue) + hF * (qfalse,qfalse) :: qb*qb;
これをコンパイルすると、TCirc {inT = {}, outT = (Q1 :<*> Q2) :<*> Q2, hpS = 2, gbS = 0, circ = Seq (Seq (Seq (Par (Hadamard) (Wire [0])) (Cond (Not) (Rot (1.0 :+ 0.0,0.0 :+ 0.0) (0.0 :+ 0.0,(-1.0) :+ -0.0)))) (Wire [1,0])) (Wire [1,0])}が得られる。
これまでの例と違っていて、通常の入力がないかわりに hpS = 2 で 2 qubit のヒープを必要とする回路になっている。ここでヒープと言っているのは単に qfalse で初期化された入力。
ここで、回路中の Par φ ψ は φ⊗ψ で回路を縦に並べたもの。 また、Cond φ ψ は (true, x) を (true, φ x) に、(false, x) を (false, ψ x) に写像する変換。
Hadamard を H、Not を X、Rot (1,0) (0,-1) を Z と書くことにすると、Eprは以下のように図示される。
![[EPRの図]](./images/20080823_0.png)
Bnmeas
Bnmeas (x,qb) (y,qb) |- let (xa,ya) = CNot (x,y)
in (Had (xa),ya) :: qb*qb;
Bnmeas は TCirc {inT = {Q2,Q2}, outT = (Q1 :<*> Q2) :<*> Q2, hpS = 0, gbS = 0, circ = Seq (Seq (Seq (Controlled-Not) (Wire [1,0])) (Wire [1,0])) (Par (Seq (Rot (0.7071067811865475 :+ 0.0,0.7071067811865475 :+ 0.0) ((-0.7071067811865475) :+ -0.0,0.7071067811865475 :+ 0.0)) (Not)) (Wire [0]))} になる。
上のアダマール変換のときの変換結果がそのまま入っているので長いけど、結局、以下の図で書ける。
![[Bnmeasの図]](./images/20080823_1.png)
U
-- The correction operations
Uol (x,qb) |- ifo x then qfalse else qtrue :: qb;
Ulo (x,qb) |- ifo x then -qtrue else qfalse :: qb;
Ull (x,qb) |- ifo x then -qfalse else qtrue :: qb;
-- The "unitary correction"
U (q,qb) (xy,qb*qb) |- let (x,y) = xy
in if x then (if y then Ull (q) else Ulo (q))
else (if y then Uol (q) else q) :: qb;
このUの場合には TCirc {inT = {Q2 :<*> Q2,Q2}, outT = Q1 :<*> Q2, hpS = 0, gbS = 2, circ = Seq (Seq (Wire [1,2,0]) (Cond (Seq (Cond (Seq (Rot ((-1.0) :+ -0.0,0.0 :+ 0.0) (0.0 :+ 0.0,1.0 :+ 0.0)) (Not)) (Seq (Rot (0.0 :+ 0.0,1.0 :+ 0.0) ((-1.0) :+ -0.0,0.0 :+ 0.0)) (Not))) (Wire [1,0])) (Seq (Controlled-Not) (Wire [1,0])))) (Wire [1,0,2])} にコンパイルされる。gbS = 2 なので本来の出力の他に 2 qubit のゴミが出ている。
Uの回路全体を考える前にまず部品から考えると、Uol, Ulo, Ull はそれぞれ以下のユニタリー変換にコンパイルされている。
![\[U_{01} = X = \left( \begin{array}{rr} 0 & 1 \\ 1 & 0 \end{array} \right)\]](tex/4c48e9697194294c7db020c47783a300.png "\[U_{01} = X = \left( \begin{array}{rr} 0 & 1 \\ 1 & 0 \end{array} \right)\]")
![\[U_{10} = Z = \left( \begin{array}{rr} 1 & 0 \\ 0 & -1 \end{array} \right)\]](tex/68a939d7e899c47a8d06f57276533f48.png "\[U_{10} = Z = \left( \begin{array}{rr} 1 & 0 \\ 0 & -1 \end{array} \right)\]")
![\[U_{11} = \left( \begin{array}{rr} 0 & 1 \\ -1 & 0 \end{array} \right)\]](tex/3499c80123b5dc41cc82921cc2f025b2.png "\[U_{11} = \left( \begin{array}{rr} 0 & 1 \\ -1 & 0 \end{array} \right)\]")
U全体はこれらを使った以下のような回路になる。
![[Uの回路図]](./images/20080823_2.png)
ここで、┤による終端が観測を表していて、観測結果がゴミになっている。観測が条件分岐よりも後になっているのは、The principle of deferred measurement を利用したものだろう。 しかし、この回路を見ると条件分岐がそのまま翻訳されているのがわかって、わかりやすいな。
Tele
-- The Teleport algorithm
Tele (a,qb) |- let (b,c) = Epr ()
in let f = Bnmeas (a,b)
in U (c,f) :: qb;
このTeleportをコンパイルすると TCirc {inT = {Q2}, outT = Q1 :<*> Q2, hpS = 2, gbS = 2, circ = ... } となる。流石に長くなるのでcircの式は省略。hsS = 2 なので 2 qubit のヒープを必要として、gbS = 2 なので本来の計算結果の他に 2 qubit がゴミとして出力されるような回路を表している。
回路本体は、既にコンパイルした Epr, Bnmeas, U を利用して以下の図のように表せる。
![[Teleの図]](./images/20080823_3.png)
まとめ
QMLで書かれた量子テレポーテーションのプログラムの量子ゲートへのコンパイルを適当に眺めてみた。 特に結論めいたものは何もないのだけど、量子計算というものがどんな感じのものなのか、ちょっと雰囲気は分かってきた気がする。
2008-08-24 [長年日記]
λ. 量子テレポーテーションの行列計算
QMLから量子回路へのコンパイルでは以下のTeleのコンパイル結果の量子ゲートを見てみた。
-- The Teleport algorithm
Tele (a,qb) |- let (b,c) = Epr ()
in let f = Bnmeas (a,b)
in U (c,f) :: qb;
結果は1qubitの入出力に加えて、2qubitのヒープと2qubitのゴミがある回路だったのだけど、ヒープの初期化と最後の観測を除いた回路本体は3qubitの入出力を持つ回路になっている。この部分はユニタリー変換になっているはずなので、行列に変換してみる。
Prelude QML> s <- readFile "teleport.qml" Prelude QML> let QAux.OK tele = pTCirc "Tele" s Prelude QML> QCirc.comp (QTyCirc.circ tele) OK Row/Input Arity = 3, Column/Output Arity = 3, ([True,True,True],[False,True,True],0.4999999999999999 :+ 0.0) ([True,True,True],[False,True,False],0.4999999999999999 :+ 0.0) ([True,True,True],[False,False,True],(-0.4999999999999999) :+ 0.0) ([True,True,True],[False,False,False],(-0.4999999999999999) :+ 0.0) ([True,True,False],[True,True,True],0.4999999999999999 :+ 0.0) ([True,True,False],[True,True,False],(-0.4999999999999999) :+ 0.0) ([True,True,False],[True,False,True],0.4999999999999999 :+ 0.0) ([True,True,False],[True,False,False],(-0.4999999999999999) :+ 0.0) ([True,False,True],[False,True,True],0.4999999999999999 :+ 0.0) ([True,False,True],[False,True,False],(-0.4999999999999999) :+ 0.0) ([True,False,True],[False,False,True],(-0.4999999999999999) :+ 0.0) ([True,False,True],[False,False,False],0.4999999999999999 :+ 0.0) ([True,False,False],[True,True,True],0.4999999999999999 :+ 0.0) ([True,False,False],[True,True,False],0.4999999999999999 :+ 0.0) ([True,False,False],[True,False,True],0.4999999999999999 :+ 0.0) ([True,False,False],[True,False,False],0.4999999999999999 :+ 0.0) ([False,True,True],[True,True,True],0.4999999999999999 :+ 0.0) ([False,True,True],[True,True,False],0.4999999999999999 :+ 0.0) ([False,True,True],[True,False,True],(-0.4999999999999999) :+ 0.0) ([False,True,True],[True,False,False],(-0.4999999999999999) :+ 0.0) ([False,True,False],[False,True,True],(-0.4999999999999999) :+ 0.0) ([False,True,False],[False,True,False],0.4999999999999999 :+ 0.0) ([False,True,False],[False,False,True],(-0.4999999999999999) :+ 0.0) ([False,True,False],[False,False,False],0.4999999999999999 :+ 0.0) ([False,False,True],[True,True,True],(-0.4999999999999999) :+ 0.0) ([False,False,True],[True,True,False],0.4999999999999999 :+ 0.0) ([False,False,True],[True,False,True],0.4999999999999999 :+ 0.0) ([False,False,True],[True,False,False],(-0.4999999999999999) :+ 0.0) ([False,False,False],[False,True,True],0.4999999999999999 :+ 0.0) ([False,False,False],[False,True,False],0.4999999999999999 :+ 0.0) ([False,False,False],[False,False,True],0.4999999999999999 :+ 0.0) ([False,False,False],[False,False,False],0.4999999999999999 :+ 0.0)
げ、QMLって内部的には横ベクトル使ってるの? まあ、今更記法を変えるのもアレなので、縦ベクトルに対する線形写像としての行列で書くと、以下のような行列が得られる。
![\[U = \frac{1}{2} \left( \begin{array}{rrrrrrrr} 1 & 0 & 1 & 0 & 0 & 1 & 0 & -1 \\ 1 & 0 & -1 & 0 & 0 & -1 & 0 & -1 \\ 1 & 0 & 1 & 0 & 0 & -1 & 0 & 1 \\ 1 & 0 & -1 & 0 & 0 & 1 & 0 & 1 \\ 0 & -1 & 0 & -1 & 1 & 0 & -1 & 0 \\ 0 & 1 & 0 & -1 & 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 & 1 & 0 & -1 & 0 \\ 0 & -1 & 0 & 1 & 1 & 0 & 1 & 0 \\ \end{array} \right)\]](tex/0083811d33d5acfaa49aaa5fef30b04e.png "\[U = \frac{1}{2} \left( \begin{array}{rrrrrrrr} 1 & 0 & 1 & 0 & 0 & 1 & 0 & -1 \\ 1 & 0 & -1 & 0 & 0 & -1 & 0 & -1 \\ 1 & 0 & 1 & 0 & 0 & -1 & 0 & 1 \\ 1 & 0 & -1 & 0 & 0 & 1 & 0 & 1 \\ 0 & -1 & 0 & -1 & 1 & 0 & -1 & 0 \\ 0 & 1 & 0 & -1 & 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 & 1 & 0 & -1 & 0 \\ 0 & -1 & 0 & 1 & 1 & 0 & 1 & 0 \\ \end{array} \right)\]")
これを (α|0〉 + β|1〉)⊗|00〉 に作用させると、以下のようになり、確かに入力の1qubitはそのまま保たれていて、さらにヒープの2qubitが計算後にはゴミになっていることがわかる。
U ((α|0〉 + β|1〉)⊗|00〉)
= U ((α|000〉 + β|100〉)
= (1/2) (α(|000〉 + |001〉 + |010〉 + |011〉) + β(|100〉 + |101〉 + |110〉 + |111〉))
= (α|0〉 + β|1〉) ⊗ (1/2)(|00〉 + |01〉 + |10〉 + |11〉)
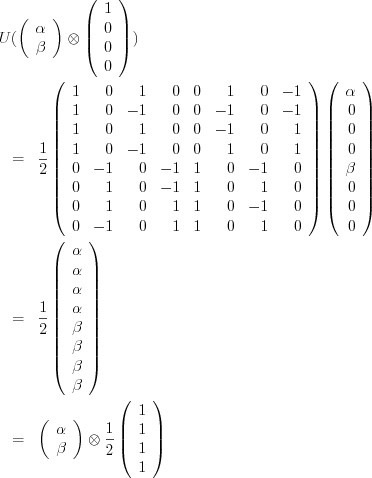
ただ、これだけ見ていると、ヒープとゴミがある分、どうしても恒等写像という感じじゃないんだよなぁ。
こうなってしまうのは、有限次元ヒルベルト空間とユニタリー変換のなす圏を暗黙に考えていたせいで、ユニタリー変換でない「観測」や「ヒープの初期化」を圏の内部では扱えないというのが原因だろう。 QML: A functional quantum programming language によれば、ヒープの初期化を扱うためには射 f : A→B をユニタリー変換からisometryに一般化した圏を考える必要があり、観測を扱うにはさらに射 f : A→B をA上の密度行列からB上の密度行列へのsuperoperatorへと一般化した圏を考える必要があるそうだ。
QMLにはそれらへのコンパイル機能もあるようなので、それもまた今度試してみたい。
2008-08-25 [長年日記]
λ. Q-circuit
Q-circuit is a macro package for drawing quantum circuit diagrams in LaTeX. On this page you'll find everything you need to start making quantum circuit diagrams of your own.
TeX で量子回路の図を書くのに便利そうな Q-circuit というのがあった。QMLから量子回路へのコンパイルでの回路図も基本的にこれで書こうとしたのだけど、どうも白丸が化けてしまう。困った……
私の環境でのQcircuitDemoの出力
![[私の環境での出力]](./images/20080825_0.png)
QcircuitDemoの期待される出力
![[期待される出力]](./images/20080825_1.png)
2008-08-26 [長年日記]
λ. QMLからIsometryへの変換
量子テレポーテーションの行列計算 で、ヒープの初期化を扱うためには、射 f : A→B をユニタリ変換からisometryに一般化した圏を考える必要があるらしいということを書いた。
isometryとは
isometryって何かと思ったけど、QML: A functional quantum programming language の 5.4.1 FQC° as isometric operations (p.87) によれば、以下のようなものだそう。
An isometry is a completely positive, distance preserving isomorphism between metric spaces. In the case of strict quantum computations the mapping is between pure quantum states, represented in the usual way as complex-valued vectors. The distance function in quantum mechanics is given by the inner-product.
……単に距離を保存する写像くらいに思ったら、意外と条件が多いのね。
completely positive については Choi's theorem on completely positive maps に説明がある。エルミート行列でかつ固有値が非負なのが positive maps で、id⊗M が常に positive map になる M が completely positive maps 。
しかし、ヒープの生成・初期化というある意味非可逆な操作を実現するために導入したいものなのに、同型だとかエルミートだとかいうのは異様に強い条件で、明らかに変だ。
というか、どうもQMLの文脈では、単に距離を保存する線形写像という意味で使われているように思える。
コンパイル例
例によって、量子テレポーテーションのプログラム
-- The Teleport algorithm
Tele (a,qb) |- let (b,c) = Epr ()
in let f = Bnmeas (a,b)
in U (c,f) :: qb;
をコンパイルしてみると以下のようになる。
Prelude QML> runI "teleport.qml" "Tele" OK (2, Isom input = 1, Isom output = 3, ([True],[True,True,True],0.4999999999999999 :+ 0.0) ([True],[True,True,False],0.4999999999999999 :+ 0.0) ([True],[True,False,True],0.4999999999999999 :+ 0.0) ([True],[True,False,False],0.4999999999999999 :+ 0.0) ([False],[False,True,True],0.4999999999999999 :+ 0.0) ([False],[False,True,False],0.4999999999999999 :+ 0.0) ([False],[False,False,True],0.4999999999999999 :+ 0.0) ([False],[False,False,False],0.4999999999999999 :+ 0.0))
これを行列で書くと以下のようになる。
![\[M = \frac{1}{2} \left( \begin{array}{rr} 1&0\\ 1&0\\ 1&0\\ 1&0\\ 0&1\\ 0&1\\ 0&1\\ 0&1\\ \end{array} \right) = \frac{1}{2} \left( \begin{array}{rrrrrrrr} 1 & 0 & 1 & 0 & 0 & 1 & 0 & -1 \\ 1 & 0 & -1 & 0 & 0 & -1 & 0 & -1 \\ 1 & 0 & 1 & 0 & 0 & -1 & 0 & 1 \\ 1 & 0 & -1 & 0 & 0 & 1 & 0 & 1 \\ 0 & -1 & 0 & -1 & 1 & 0 & -1 & 0 \\ 0 & 1 & 0 & -1 & 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 & 1 & 0 & -1 & 0 \\ 0 & -1 & 0 & 1 & 1 & 0 & 1 & 0 \\ \end{array} \right) \left( \begin{array}{rr} 1&0\\ 0&0\\ 0&0\\ 0&0\\ 0&1\\ 0&0\\ 0&0\\ 0&0\\ \end{array} \right) = U\circ(-\otimes|00\rangle)\]](tex/524d11878e924a9ad44cb8fccedb145c.png "\[M = \frac{1}{2} \left( \begin{array}{rr} 1&0\\ 1&0\\ 1&0\\ 1&0\\ 0&1\\ 0&1\\ 0&1\\ 0&1\\ \end{array} \right) = \frac{1}{2} \left( \begin{array}{rrrrrrrr} 1 & 0 & 1 & 0 & 0 & 1 & 0 & -1 \\ 1 & 0 & -1 & 0 & 0 & -1 & 0 & -1 \\ 1 & 0 & 1 & 0 & 0 & -1 & 0 & 1 \\ 1 & 0 & -1 & 0 & 0 & 1 & 0 & 1 \\ 0 & -1 & 0 & -1 & 1 & 0 & -1 & 0 \\ 0 & 1 & 0 & -1 & 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 & 1 & 0 & -1 & 0 \\ 0 & -1 & 0 & 1 & 1 & 0 & 1 & 0 \\ \end{array} \right) \left( \begin{array}{rr} 1&0\\ 0&0\\ 0&0\\ 0&0\\ 0&1\\ 0&0\\ 0&0\\ 0&0\\ \end{array} \right) = U\circ(-\otimes|00\rangle)\]")
これは量子テレポーテーションの行列計算で得られたユニタリー変換Uに、ヒープの生成・初期化に相当するisometry -⊗|00〉 : Q2 → Q2⊗Q2 を結合したisometry ![\xymatrix{Q_2 \ar[r]^-{-\otimes|00\rangle} & Q_2\otimes Q_2\otimes Q_2 \ar[r]^-{U} & Q_2\otimes Q_2\otimes Q_2}](tex/a5985107bd7ce19ee2a3f5c88312f3fc.png "\xymatrix{Q_2 \ar[r]^-{-\otimes|00\rangle} & Q_2\otimes Q_2\otimes Q_2 \ar[r]^-{U} & Q_2\otimes Q_2\otimes Q_2}")
になっている。
まとめ
Q2⊗Q2⊗Q2→Q2⊗Q2⊗Q2 から、 Q2→Q2⊗Q2⊗Q2 になって、id : Q2→Q2⊗Q2 にちょっと近づいた。後はsuperoperatorの圏に移れば、Q2→Q2にすることが出来て、idと等しくなるはず……
2008-08-27 [長年日記]
λ. “Program Generation in the Equivalent Transformation Computation Model Using the Squeeze Method” by Kiyoshi Akama, Ekawit Nantajeewarawat, and Hidekatsu Koike
あろは先生を問い詰める会の予習のために読んだ。 昔、「コンパイラ」とfull abstraction - sumiiの日記のコメント欄で Formalization of the Equivalent Transformation Computation Modelという論文を教えてもらって読んだときにはよく分からなかったけど、こっちの論文を読んでちょっと分かってきた気がする。
(後で書く)
![[カタツムリ]](./images/20080828_0.jpg)
2008-08-29 [長年日記]
λ. ETでワンのアルゴリズムを……挫折
せっかくだから、あろは先生を問い詰める会の前にETと「搾り出し方」を試してみるかと思い、昔Haskellで書いて微妙だった Wang's Algorithm (ワンのアルゴリズム) を試してみることにする。
仕様
仕様は以下の組 (D,Q) で表される。
- ホーン節で書かれた背景知識 D
- ホーン節で書かれたクエリーの集合 Q
まずは背景知識D。これは実行可能性は考えなくて良いはずなので、まあ適当にアルゴリズムではなく定義っぽい感じで。
valid(X) ← valid([], [X]). valid(Gamma, Delta)) ← member(X, Gamma), member(X, Delta). valid(Gamma, Delta) ← permutation(Gamma, Gamma1), valid(Gamma1, Delta). valid(Gamma, Delta) ← permutation(Delta, Delta1), valid(Gamma, Delta1). valid(Gamma, [and(A,B)|Delta])) ← valid(Gamma, [A|Delta]), valid(Gamma, [B|Delta]). valid(Gamma, [or(A,B)|Delta])) ← valid(Gamma, [A,B|Delta]). valid(Gamma, [not(A)|Delta])) ← valid([A|Gamma], Delta). valid([and(A,B)|Gamma, Delta)) ← valid([A,B|Gamma], Delta). valid([or(A,B)|Gamma], Delta)) ← valid([A|Gamma], Delta), valid([B|Gamma], Delta). valid([not(A)|Gamma, Delta)) ← valid(Gamma, [A|Delta]). valid(Gamma, [imply(A,B)|Delta]) ← valid(Gamma, [or(not(A),B)|Delta]). valid([imply(A,B)|Gamma], Delta) ← valid([or(not(A),B)|Gamma], Delta). member(X, [X|_]). member(X, [_|T]) ← member(X,T). permutation([], []). permutation(L, [X|L2]) ← select(X, L, L1), permutation(L1, L2). select(X, [X|L], L). select(X, [Y|L], [Y|L1]) ← select(X, L, L1).
お次はクエリーの集合Q。
prb1
ans(X) ← valid(X).
prb2
s ← valid(imply(imply(a,b), imply(imply(a,imply(b,c)), imply(a,c)))).
prb3
k ← valid(imply(a, imply(b, a))).
prb4
peirce ← valid(imply(imply(imply(p, q), p), p)).
Q = {prb1, prb2, prb3, prb4}
処理系のダウンロード
<URL:http://assam.cims.hokudai.ac.jp/et/indexj.html>
搾り出し方
早速、論文の手順に基づいて搾り出してやるぜ! と思って喜び勇んではじめたら、肝心のパターンの決定とルールの生成の部分がこの論文には書いていないのだった。しょぼーん。
もちろん、アルゴリズムを直接書くのは難しくないと思うけど、それをETでやっても仕方がないと思うし。
2008-08-31 [長年日記]
λ. あろは先生を問い詰める会 (ET Seminar)
あろは先生を問い詰める会というイベントに参加。
これはなんと、あろはさんが7時間ぶっ続けで発表し、問い詰める気満々の聴衆からすごい勢いでツッコミと質問が入るという恐ろしいイベントだった。 ツッコミまくってたお前が言うなという気もするけど。 特に、あまり本質的でない質問や、勘違いした質問を結構してしまって、そこはちょっと反省。 そんな過酷な環境にもかかわらず、長時間にわたって忍耐強く続けてくださったあろはさんには感謝するとともに賛辞を送りたい。
こないだの論文とあわせて、ETの目指すものと現状について大体理解できた気がする。
以下はとりあえず自分がした質問を中心に簡単に、感想や聞きそびれてしまったことなども含めてメモ。
命令型の理論とか仕様とか
ホワット・ア・ワンダフル・ワールド ET Q&Aでは「仕様 (what) の概念無し」、今回のスライドでも「そもそも理論が無い (あるけど，後付け （現場の要請ドリブン）)」と書いてあった。
そこで、「命令型言語でもホーア論理とかで仕様書けるし、最近JMLとか少し流行ってるよ」と聞いたら、ここで仕様と呼んでいるものは解きたい問題を記述したもので、関数の性質とかを記述したものではないとのこと。仕様をそう定義すれば確かにそうなんだけど、うーん……。
あと、他の方から「JMLとかは仕様ではなくアサーションでは」というコメントがあった。私の理解では「アサーション」は満たすべき性質の一部を記述したもので、「仕様」は満たすべき性質の全てを記述しつくしたもの。JMLはそのどちらも記述可能。
それから、命令型言語における仕様からの合成という話では、refinement calculus みたいな古典的な話もあるので、その辺りも少し質問してみたけど、仕様の概念が違うこともあって、あまり比較対象にはされていないような感じだった。
notは無理筋?
「notの定義例」のスライドでは後で書く否定の種類の方面の話に気をとられていたけど、落ち着いて考えると、ET 版の not が Prolog 版 not の問題を解決しているのか良く分からない。 というのも、結局PrologのSLD導出アルゴリズムの手続き的性質に依存していたのが、Dルールの手続き的性質に依存するようになっただけで、今回のセミナーではあまり触れられていなかったDルールの理論的扱いがわからないと何が変わったのか分からないので。
また、リファレンスマニュアルのnotの項の「(not *s)」の説明で「notは副作用を起こします。*s中の変数が実行中に変更されると、共有するnotの外側の変数も変更されます。この変更は、結果の真偽によりません」とあるけど、これはPrologの問題よりも遥かに凶悪なような気がする。 あろはさんも「条件部の結果が本体にひきずるのは問題」「実装で解決できるかも」というようなことを言っていた。
否定の種類
「notの定義例」というスライドのところで質問したが、利点として<URL:http://assam.cims.hokudai.ac.jp/et/indexj.html>に「否定を含む問題を正しく扱える」とあったのが気になっている。 Prolog でも negation as failure については問題なく扱える*1ので、これは negation as failure ではない通常の否定(classical negation とか strong negation と呼ばれる)を扱えるといっているのだろうか。
あろはさんによると、最近、DL(Description Logics) を扱う関係で ET で真の否定を扱える理論(?)が出来たとか。 論理プログラミングの文脈だと、通常の否定を扱うためには解集合プログラミング(answer set programming, ASP)のような枠組みが必要になってくるが、これは理論的にはともかく実装技術としては問題領域を限定した技術だと思う。 広い問題領域を対象としたETに対して実装されるとしたらどのような形になるのか興味深いところ。
構成的プログラミング
前日の LL Future での Lightning Talk 「超未来言語Gallina」で「仕様を効率的に実行可能な形に等価変換していくことを実現したのがGallina(Coq)」だと断言したyoshihiro503さんと、「Coq等はルールのように分解可能性のある(単体で正当性が議論できる)コンポーネントの集合で構成されているわけでない」というあろはさんとのバトルをちょっと期待してたんだけど、特にそんなことはなかった。
それはそうと、効率に関しては確かにちょっと問題はあるのかもと思うこともある。 というのも、Coqで書ける*2のは停止性が検査機によって自動的に判定出来る関数だけで、停止性が自動判定出来ない関数定義は書けないため、効率的だけど停止性が自動判定出来ない関数を書けずに問題になる場合が本当に無いのか自信がないため。Coqで“無限オブ無限”を書いたときにもちょっと思ったんだけどね。
palpal問題
ETの論文でよく出てくるpalindromeの例がpalpal問題と呼ばれてるのね。どうでもいいが、最近やっている英語版の逆転裁判で Detective Gumshoe (糸鋸刑事) が pal という呼びかけを頻繁に使っているので、それを連想してしまって、少しツボだった。
肝になる5番目のルール rv(*x, *y), rv(*x, *z) ⇒ {=(*y, *z)}, rv(*x, *y). にみんなの質問が集中していて、その結構な部分が「証明できる」が指すことについてだった気がする。
結局、このルールを自動導出出来るようになったのが最近というのは良いのだけど、「本当に厳密に D に対して ET ルールであることが証明可能になったのは，つい最近」というのが機械による自動証明だけを指しているのか、人間による証明についても不可能だったのかがよく分からなかった。
プライオリティ
これは私の勘違いでした。済みません。
(後で書く)
特殊化システムと書き換え系
「書き換え系としては多重集合の書き換え系(+情報変数)と思ってよいのか?」と聞いたら、その通りとのこと。多重集合の書き換え系なら線形論理の証明探索を書いたりするのに便利かもと思った。
それから、情報付き変数を使って特殊化システムを拡張可能とのこと。
書き換え系という意味では、Maudeの代数的仕様記述+書き換え論理という枠組みとの比較なんかも質問してみたかったが、これは質問しそびれてしまった。
圏論による定式化?
仕様空間とプログラム空間の理論は、channel theory とか chu space とか institution とか良くあるやつに似ているので、良くあるような感じで定式化してやれば良いのではないかと。 それで何か嬉しい結果が出てくるかはわからないけど。
あろはさんの研究とか
スライドにはあまり書いていないけど、私の理解では「命令型言語のプログラムの空間からETプログラム(Dルール)の空間への埋め込みを定義して、その逆変換としてDルールから命令型言語へのコンパイルを定式化」というのを一つのアプローチとして考えていたようだだった。
ただ、プログラムの埋め込みは仕様を何らかの意味で保たなくてはならないはず*3で、その部分があまり考えられていない気がして、その辺りを質問してみた。
そして、その議論からどうもDルールで副作用のあるアトム(?)の扱いが仕様上どう扱われているのかが気になりだして、それも聞いてみた。unification が substitution を生成するのと同じ扱いで、副作用については世界の枝分かれみたいな感じで扱われるとか。 ただ、一方でDルールにはNルールと違って正当性の概念がない(?)とか、どうもあまり理論的には扱われていないようでもあった。
ネタとかどうでも良い点とか
- S式版の記法で使われているasはassertの略でprolog-kr由来
- 『仕様からの合成』と要約してしまうとLyeeと同じになってしまってアレ
- 闇世界仮説。
- 高階質問状
- 「すごいパーツをいれれば僕はすごくなるよ」
他の方の感想など
- 埒を明ける日々: ET Seminar
- LLFuture と、等価変換セミナーに行ってきた - にわとり小屋でのプログラミング日記
- 等価変換理論集中セミナー2008（at 溜池某所） - ヤドカリデンキ商会（第一倉庫）
- 2008-09-03 - 兼雑記
- とりあえず俺はProlog知らなすぎだ - soutaroにっき
- <URL:http://morihyphen.hp.infoseek.co.jp/log2/200808.html#083118>
- <URL:http://page.freett.com/shelarcy/log/2008/diary_08.html#haduki312008>
- 8月31日は問い詰める会 - YasuyukiMiuraの日記
