日々の流転

λ. 今日も良い天気だな〜。

λ. C++とSingletonパターン

それは定義じゃなくてただの宣言なので、問題ないんじゃないかと(未確認)。

λ. 読んだ本

• 「金融腐蝕列島」上　高杉良
• 「金融腐蝕列島」下　高杉良
• 「処刑と拷問の世界史−どこまで人は残虐になれるのか?」　岡田英男

λ. ゲーマー?

ゲーマーの定義は知らないけど、ゲーマーと言われればゲーマーなのかも。最近あんましゲームしてないけど、ヴァンパイア・セイヴァーとか結構好きだったなぁ。あれはぜひ続編を出して欲しい。

λ. コンパイル猿

gtk_main()にたどり着いているって事は、Windowsメッセージでマズイ事になってるという可能性がありそうだ。

探してみると、glib/gmain.cのg_poll()が、G_OS_WIN32が定義されているかどうかで二つに分かれていて、ここにG_WIN32_MSG_HANDLEを処理する部分がある。ただ、ここで悩ましいのはGPollFDの扱いだよなぁ。当然今はfile descriptorが入っているのだけど……

On Win32, the fd in a GPollFD should be Win32 HANDLE (*not* a file descriptor as provided by the C runtime) that can be used by MsgWaitForMultipleObjects. This does *not* include file handles from CreateFile, SOCKETs, nor pipe handles. (But you can use WSAEventSelect to signal events when a SOCKET is readable).

On Win32, fd can also be the special value G_WIN32_MSG_HANDLE to indicate polling for messages. These message queue GPollFDs should be added with the g_main_poll_win32_msg_add function.

But note that G_WIN32_MSG_HANDLE GPollFDs should not be used by GDK (GTK) programs, as GDK itself wants to read messages and convert them to GDK events.

So, unless you really know what you are doing, it's best not to try to use the main loop polling stuff for your own needs on Win32. It's really only written for the GIMP's needs so far.

さて、fdtab[fd]->get_handle() で Cygwin の file descriptor から Win32のHANDLEを得られると考えて良いとしたら、select()は使わないで、全部HANDLEに変換してMsgWaitForMultipleObjects()するのが良いかもしれない。しかし、fhandler_baseのget_handle(), get_io_handle(), get_output_handle() はどう使い分ければ良いのだろう。……と思ったら、これらはcygwin1.dll内部専用か。ちぇっ。

というか、そもそもCygwinは自前のpoll()を持っているので、glib/gmain.cのg_poll()は最初から使われていなかったのね。g_poll()をいじってどうこうしようとしてたのはそもそも筋が悪かったわけか。

gdk/win32/gdkevent-win32.cの方でGSourceをもっとちゃんと使えば、多少効率は落ちても、poll()の置き換えなしに出来るんじゃないかという気もする。この辺りのソースをきちんと読まないといかんかなぁ……

λ. PRIMES is in P

今更だけど印刷してみた。僕の周りでは概ね好意的な反応ばかりなので、あけてくれ日記 2002.08.17(土) の「真っ赤な嘘」という記述が気になっています。

λ. 論文読み会

"Personalization in Distributed e-Learning Environments"

Peter Dolog, Michael Sintek

"Opportunity Knocks: a System to Provide Cognitive Assistance with Transportation Services."

D. J. Patterson, L. Liao, K. Gajos, M. Collier, N. Livic, K. Olson, S. Wang, D. Fox, and H. Kautz

λ. バグ

デスクトップPCの裏をいじっていたら、なぜか虫の死骸を発見。これは百足?

(追記) 関係ないけど、ムカデ様との闘いというブログを発見した。

λ. ラップトップのHDDの調子が悪い

ラップトップ(Let's note CF-T1)のHDDの調子が悪い。休止状態から復元するときに読み取りエラーが頻発している感じで、復元できない。けど、普通に起動する分には平気だし、休止状態にするときも何も問題ない。あと、チェックディスクしても不良セクタが見つからないだけでなく、読み取りエラーが起こっているような様子もなかった。良く分からん。

LLDNの直前なのに困ったものだ。いまから修理に出してたら間に合わないし、とりあえずLLDNが終わるまでは何とかごまかすか。でも休止状態から復元できないのは不便だ……

あと、このHDD(TOSHIBA MK4020GLS)は容量が40GBしかないから、自分でもっとデカイ容量のHDDを買ってきて取り替えようかとも思ったけど、なにやら難しそうだ。

参考になりそうなページ

• 湯上りのPC改造記 : NOTE PC HDD置換顛末記
• ロジック電圧3.3VノートのHDD換装実験
• Let's note「CF-T1」で遊ぼう, Let's note「CF-R1」で遊ぼう
• Let's Note Y2 80GB HDD 換装
• http://cgi.mobile-pc.com/pc/sat/letshdd2.html

λ. 『陰陽ノ京〈巻の4〉』 渡瀬 草一郎

を読んだ。

λ. Re: Haskellのリストの定義

はてなのアカウントを持っていないとコメント出来ないようなのでこっちに。

Haskellでは a = 1 : a のような定義も許され*1、リスト型は値として無限リストも含みます。なので、<URL:http://d.hatena.ne.jp/yoriyuki/20060808/p1> については、そもそも「型の解釈としてはList型は有限List」ではないので、何もややこしいことは無いです。

また、sumiiさん*2が<URL:http://d.hatena.ne.jp/yoriyuki/20060808#c1156214112>で「Haskellなどでは（SMLなどと同様に構成された意味論では）始代数にはならないのではないかと思います」とコメントしていますが、リスト型が無限リストを含むことは始代数として解釈されることと矛盾しません。私も以前に「Haskellの代数的データ型は始代数ではない」というエントリを書きましたが、これは勘違いで、リストや他の多くのデータ型*3は、CPO*4と連続関数を使った通常の意味論では始代数になっているはずです。 というのも、リスト型が関手 F(X) = (A×X)+1 *5 の終余代数になっている事は比較的簡単に示す事が出来、さらに任意の f:X->Y に対して F(f) が正格なので、20040731#p07の定理2から F の始代数になるはずなので。

λ. 幻のハワイ日本連合 〜カラカウア王・祖国防衛に賭けた生涯〜 (その時歴史が動いた)

心苦しくはあるけど、当時の日本の判断としては妥当だったのではないかと思う。それから、カイウラニ(Kaʻiulani)王女萌え、とか思ったら、<URL:http://www.legendaryhawaii.com/lady/lady02.htm>によると当時はまだ5歳だったとか。ちょっとしょぼーん。

λ. IPA未踏ソフトウェア創造事業2006年度下期千葉PM採択プロジェクト最終成果報告会

未踏千葉PM採択の4案件について、事業の最終成果報告を行う。形式はスクール形式の会場において、プレゼンテーションおよび質疑応答とする。4案件は、「SELinuxによるPostgreSQLのアクセス制御強化」、「Ruby用仮想マシンYARVの完成度向上」、「ウェアラブルコンピューティングのためのイベント駆動型ミドルウェア開発」、「Web上で動作するモデリング環境 Kodougu の開発」である。

今回4案件の報告それぞれについて関連深い分野より著名ゲストを招き、入門者にも深く配慮したチュートリアル等の実践的セッションを行っていただくこととした。千葉PM登壇のパネルディスカッションと併せ、現在最新の技術潮流を解説していく。

<URL:http://www.atdot.net/~ko1/diary/200708.html#d22> より。 おお、面白そう。 会社休んで行こうかしら。 ……と思ってたら、(仕事上の)予定が入ってしまった。残念。

あと、笹田さんの写真がカッコイイ。

λ. QMLから量子回路へのコンパイル

QMLで量子テレポーテーションの続きで、QMLのプログラムを実際にコンパイルして遊んでみる。出力先は色々選べるが、とりあえず型付きの量子回路へのコンパイルを試してみることに。qml.hsをghciで読み込んで、runTC "ファイル名" "識別子" とすれば、型付きの量子回路へと変換される。

Qnot

-- The quantum Not operation (Pauli X)
Qnot (b,qb) |- ifo b then qfalse else qtrue :: qb;

まずはこのQnotをコンパイルしてみる。

Prelude QML> runTC "teleport.qml" "Qnot"
OK (TCirc {inT = {Q2}, outT = Q1 :<*> Q2, hpS = 0, gbS = 0, circ = Not})

inT が入力の「文脈」を表していて、outTは出力の「型」を表している。ただ、単なる Q2 ではなく Q1⊗Q2 になっているのは何でなんだろう。Q1⊗Q2 ≅ Q2 なので、構わないといえば構わないのだけど。

それから、hpS = 0 はヒープのサイズが 0 qubit で inT 以外の余計な領域を必要としないことを、gbS = 0 はゴミのサイズが 0 qubit で余計なゴミが出力されないことを表している。circ が回路本体で、ここでは単純なNotゲートになっている。

アダマール変換

-- The Hadamard operation
Had (b,qb) |- ifo b then hF * qfalse + (-hF) * qtrue
                    else hF * qfalse + hF * qtrue :: qb;

次にアダマール変換 Had の場合には「TCirc {inT = {Q2}, outT = Q1 :<*> Q2, hpS = 0, gbS = 0, circ = Seq (Rot (0.7071067811865475 :+ 0.0,0.7071067811865475 :+ 0.0) ((-0.7071067811865475) :+ -0.0,0.7071067811865475 :+ 0.0)) (Not)}」が得られる。

ここで、Rot (λ0, λ1) (κ0, κ1) は以下で定義されるユニタリー変換を表しているようだ。

• qfalse ↦ λ0 qfalse + λ1 qtrue
• qtrue ↦ κ0 qfalse + κ1 qtrue

これを行列で表すと になる。 Had の出力に現れる Rot の場合には、 という行列を表している。

そして、Seq φ ψ は ψ ∘ φ という合成を表しているようだ。

Not も内部的には Rot (0,1) (1,0) で表現されているので、行列で表して計算してみると、通常のアダマール変換(Hadamard transform)になっているのが確認できる。

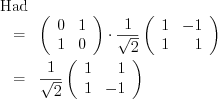
EPR

-- The constant EPR pair
Epr |- hF * (qtrue,qtrue) + hF * (qfalse,qfalse) :: qb*qb;

これをコンパイルすると、TCirc {inT = {}, outT = (Q1 :<*> Q2) :<*> Q2, hpS = 2, gbS = 0, circ = Seq (Seq (Seq (Par (Hadamard) (Wire [0])) (Cond (Not) (Rot (1.0 :+ 0.0,0.0 :+ 0.0) (0.0 :+ 0.0,(-1.0) :+ -0.0)))) (Wire [1,0])) (Wire [1,0])}が得られる。

これまでの例と違っていて、通常の入力がないかわりに hpS = 2 で 2 qubit のヒープを必要とする回路になっている。ここでヒープと言っているのは単に qfalse で初期化された入力。

ここで、回路中の Par φ ψ は φ⊗ψ で回路を縦に並べたもの。 また、Cond φ ψ は (true, x) を (true, φ x) に、(false, x) を (false, ψ x) に写像する変換。

Hadamard を H、Not を X、Rot (1,0) (0,-1) を Z と書くことにすると、Eprは以下のように図示される。

Bnmeas

Bnmeas (x,qb) (y,qb) |- let (xa,ya) = CNot (x,y)
                        in  (Had (xa),ya) :: qb*qb;

Bnmeas は TCirc {inT = {Q2,Q2}, outT = (Q1 :<*> Q2) :<*> Q2, hpS = 0, gbS = 0, circ = Seq (Seq (Seq (Controlled-Not) (Wire [1,0])) (Wire [1,0])) (Par (Seq (Rot (0.7071067811865475 :+ 0.0,0.7071067811865475 :+ 0.0) ((-0.7071067811865475) :+ -0.0,0.7071067811865475 :+ 0.0)) (Not)) (Wire [0]))} になる。

上のアダマール変換のときの変換結果がそのまま入っているので長いけど、結局、以下の図で書ける。

U

-- The correction operations
Uol (x,qb) |- ifo x then  qfalse else qtrue  :: qb; 
Ulo (x,qb) |- ifo x then -qtrue  else qfalse :: qb;
Ull (x,qb) |- ifo x then -qfalse else qtrue  :: qb;  

-- The "unitary correction"
U (q,qb) (xy,qb*qb) |- let (x,y) = xy 
                       in if x then (if y then Ull (q) else Ulo (q))
                               else (if y then Uol (q) else q) :: qb;

このUの場合には TCirc {inT = {Q2 :<*> Q2,Q2}, outT = Q1 :<*> Q2, hpS = 0, gbS = 2, circ = Seq (Seq (Wire [1,2,0]) (Cond (Seq (Cond (Seq (Rot ((-1.0) :+ -0.0,0.0 :+ 0.0) (0.0 :+ 0.0,1.0 :+ 0.0)) (Not)) (Seq (Rot (0.0 :+ 0.0,1.0 :+ 0.0) ((-1.0) :+ -0.0,0.0 :+ 0.0)) (Not))) (Wire [1,0])) (Seq (Controlled-Not) (Wire [1,0])))) (Wire [1,0,2])} にコンパイルされる。gbS = 2 なので本来の出力の他に 2 qubit のゴミが出ている。

Uの回路全体を考える前にまず部品から考えると、Uol, Ulo, Ull はそれぞれ以下のユニタリー変換にコンパイルされている。

U全体はこれらを使った以下のような回路になる。

ここで、┤による終端が観測を表していて、観測結果がゴミになっている。観測が条件分岐よりも後になっているのは、The principle of deferred measurement を利用したものだろう。 しかし、この回路を見ると条件分岐がそのまま翻訳されているのがわかって、わかりやすいな。

Tele

-- The Teleport algorithm
Tele (a,qb) |- let (b,c) = Epr () 
               in  let f = Bnmeas (a,b)
                   in U (c,f) :: qb;

このTeleportをコンパイルすると TCirc {inT = {Q2}, outT = Q1 :<*> Q2, hpS = 2, gbS = 2, circ = ... } となる。流石に長くなるのでcircの式は省略。hsS = 2 なので 2 qubit のヒープを必要として、gbS = 2 なので本来の計算結果の他に 2 qubit がゴミとして出力されるような回路を表している。

回路本体は、既にコンパイルした Epr, Bnmeas, U を利用して以下の図のように表せる。

まとめ

QMLで書かれた量子テレポーテーションのプログラムの量子ゲートへのコンパイルを適当に眺めてみた。 特に結論めいたものは何もないのだけど、量子計算というものがどんな感じのものなのか、ちょっと雰囲気は分かってきた気がする。

λ. Real World Haskell読書会 2009-08

衆院選の期日前投票を済ませてからRWH読書会に参加。 今回は6章「型クラスを使う」から7章「入出力」の7.2「ファイルおよびハンドルを使う」まで。型クラス周りはHaskell98に対する色々な拡張があるので、それらの関係がやはりややこしいと思った。 それから、6.9「重複インスタンスのないJSON型クラス」のmapEitherはmapMを使えばいいじゃんと思ったが、モナドはまだ出てきてないのだった。が、その割にはControl.Arrowのsecondを使っていたりして、なんというか……

• Chapter 6. Using Typeclasses (原著オンライン版)
• Chapter 7. Input and output (原著オンライン版)
• 前回

λ. CLTT の 1.4 Cloven and split fibrations のノート

CLTT読書会で読んでいる Categorical Logic and Type Theory の、1.4 Cloven and split fibrations を復習して、練習問題も一通り解いた。

• ノート