2008-08-24 [長年日記]
λ. 量子テレポーテーションの行列計算
QMLから量子回路へのコンパイルでは以下のTeleのコンパイル結果の量子ゲートを見てみた。
-- The Teleport algorithm
Tele (a,qb) |- let (b,c) = Epr ()
in let f = Bnmeas (a,b)
in U (c,f) :: qb;
結果は1qubitの入出力に加えて、2qubitのヒープと2qubitのゴミがある回路だったのだけど、ヒープの初期化と最後の観測を除いた回路本体は3qubitの入出力を持つ回路になっている。この部分はユニタリー変換になっているはずなので、行列に変換してみる。
Prelude QML> s <- readFile "teleport.qml" Prelude QML> let QAux.OK tele = pTCirc "Tele" s Prelude QML> QCirc.comp (QTyCirc.circ tele) OK Row/Input Arity = 3, Column/Output Arity = 3, ([True,True,True],[False,True,True],0.4999999999999999 :+ 0.0) ([True,True,True],[False,True,False],0.4999999999999999 :+ 0.0) ([True,True,True],[False,False,True],(-0.4999999999999999) :+ 0.0) ([True,True,True],[False,False,False],(-0.4999999999999999) :+ 0.0) ([True,True,False],[True,True,True],0.4999999999999999 :+ 0.0) ([True,True,False],[True,True,False],(-0.4999999999999999) :+ 0.0) ([True,True,False],[True,False,True],0.4999999999999999 :+ 0.0) ([True,True,False],[True,False,False],(-0.4999999999999999) :+ 0.0) ([True,False,True],[False,True,True],0.4999999999999999 :+ 0.0) ([True,False,True],[False,True,False],(-0.4999999999999999) :+ 0.0) ([True,False,True],[False,False,True],(-0.4999999999999999) :+ 0.0) ([True,False,True],[False,False,False],0.4999999999999999 :+ 0.0) ([True,False,False],[True,True,True],0.4999999999999999 :+ 0.0) ([True,False,False],[True,True,False],0.4999999999999999 :+ 0.0) ([True,False,False],[True,False,True],0.4999999999999999 :+ 0.0) ([True,False,False],[True,False,False],0.4999999999999999 :+ 0.0) ([False,True,True],[True,True,True],0.4999999999999999 :+ 0.0) ([False,True,True],[True,True,False],0.4999999999999999 :+ 0.0) ([False,True,True],[True,False,True],(-0.4999999999999999) :+ 0.0) ([False,True,True],[True,False,False],(-0.4999999999999999) :+ 0.0) ([False,True,False],[False,True,True],(-0.4999999999999999) :+ 0.0) ([False,True,False],[False,True,False],0.4999999999999999 :+ 0.0) ([False,True,False],[False,False,True],(-0.4999999999999999) :+ 0.0) ([False,True,False],[False,False,False],0.4999999999999999 :+ 0.0) ([False,False,True],[True,True,True],(-0.4999999999999999) :+ 0.0) ([False,False,True],[True,True,False],0.4999999999999999 :+ 0.0) ([False,False,True],[True,False,True],0.4999999999999999 :+ 0.0) ([False,False,True],[True,False,False],(-0.4999999999999999) :+ 0.0) ([False,False,False],[False,True,True],0.4999999999999999 :+ 0.0) ([False,False,False],[False,True,False],0.4999999999999999 :+ 0.0) ([False,False,False],[False,False,True],0.4999999999999999 :+ 0.0) ([False,False,False],[False,False,False],0.4999999999999999 :+ 0.0)
げ、QMLって内部的には横ベクトル使ってるの? まあ、今更記法を変えるのもアレなので、縦ベクトルに対する線形写像としての行列で書くと、以下のような行列が得られる。
![\[U = \frac{1}{2} \left( \begin{array}{rrrrrrrr} 1 & 0 & 1 & 0 & 0 & 1 & 0 & -1 \\ 1 & 0 & -1 & 0 & 0 & -1 & 0 & -1 \\ 1 & 0 & 1 & 0 & 0 & -1 & 0 & 1 \\ 1 & 0 & -1 & 0 & 0 & 1 & 0 & 1 \\ 0 & -1 & 0 & -1 & 1 & 0 & -1 & 0 \\ 0 & 1 & 0 & -1 & 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 & 1 & 0 & -1 & 0 \\ 0 & -1 & 0 & 1 & 1 & 0 & 1 & 0 \\ \end{array} \right)\] \[U = \frac{1}{2} \left( \begin{array}{rrrrrrrr} 1 & 0 & 1 & 0 & 0 & 1 & 0 & -1 \\ 1 & 0 & -1 & 0 & 0 & -1 & 0 & -1 \\ 1 & 0 & 1 & 0 & 0 & -1 & 0 & 1 \\ 1 & 0 & -1 & 0 & 0 & 1 & 0 & 1 \\ 0 & -1 & 0 & -1 & 1 & 0 & -1 & 0 \\ 0 & 1 & 0 & -1 & 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 & 1 & 0 & -1 & 0 \\ 0 & -1 & 0 & 1 & 1 & 0 & 1 & 0 \\ \end{array} \right)\]](tex/0083811d33d5acfaa49aaa5fef30b04e.png)
これを (α|0〉 + β|1〉)⊗|00〉 に作用させると、以下のようになり、確かに入力の1qubitはそのまま保たれていて、さらにヒープの2qubitが計算後にはゴミになっていることがわかる。
U ((α|0〉 + β|1〉)⊗|00〉)
= U ((α|000〉 + β|100〉)
= (1/2) (α(|000〉 + |001〉 + |010〉 + |011〉) + β(|100〉 + |101〉 + |110〉 + |111〉))
= (α|0〉 + β|1〉) ⊗ (1/2)(|00〉 + |01〉 + |10〉 + |11〉)
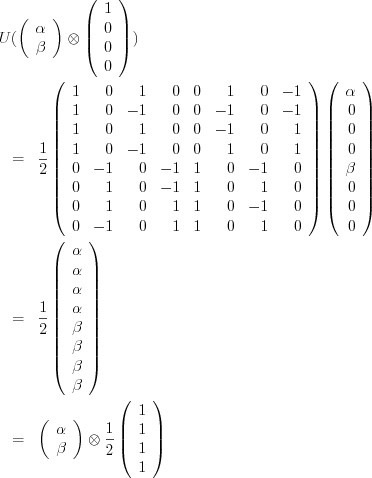
ただ、これだけ見ていると、ヒープとゴミがある分、どうしても恒等写像という感じじゃないんだよなぁ。
こうなってしまうのは、有限次元ヒルベルト空間とユニタリー変換のなす圏を暗黙に考えていたせいで、ユニタリー変換でない「観測」や「ヒープの初期化」を圏の内部では扱えないというのが原因だろう。 QML: A functional quantum programming language によれば、ヒープの初期化を扱うためには射 f : A→B をユニタリー変換からisometryに一般化した圏を考える必要があり、観測を扱うにはさらに射 f : A→B をA上の密度行列からB上の密度行列へのsuperoperatorへと一般化した圏を考える必要があるそうだ。
QMLにはそれらへのコンパイル機能もあるようなので、それもまた今度試してみたい。
