トップ «前の日(08-23) 最新 次の日(08-25)» 追記

日々の流転

2001-08-24

λ. 最近は、なにやら脈絡の無い夢が多い。その不可解さがいらだたしい。

λ. Script-Fu メニューでもアイコン表示 (from 他力本願な日記・改)

gimp メニューにアイコン表示が更に進化。すげーぜ。よし、Ruby-FuにもRF_MENUICONを追加するか。どうせRF_PREVIEWも考えてたし、引数情報以外も登録できるようにしておくと、何かと良いかも知れん。

Tags: gimp

ちなみに、以下のようにあるけど、MenuItemウィジェットには任意のウィジェットを張り付けることが出来るので、その機能が提供されないItemFactoryをGNOMEが使ってないって事だと思う。

とここまでやってから気づいたのですが，Gnome のパネルのメニューにはそれぞれの項目のアイコン画像が貼り込まれているんですね．テキストの列揃えもできています．その機構を持ってくればよかったのかも．．．Gtk にはこの機能はないようだったんですが，それに基づいているはずの Gnome ではどうやって実現しているのでしょうか？

λ. URLメモ

λ. メルマガ「小泉純一郎を斬る！」

の第4号で興味深い事が書いてあった。以下に部分的に引用しよう。

いいかえれば、冷戦とは民族解放運動封じ込めの体制として成立し、ソ連(スターリン主義)はその体制の補完物としての役割を果たしたのである。

日本をめぐっても同様のことが言える。アメリカは冷戦下で、日本を日米同盟−西側陣営に組み込むために、中国市場に代わる市場として東南アジアを日本に提供することを構想し、東南アジア諸国の日本に対する戦争賠償要求の抑え込みを図った。そして、38度線での冷戦対峙の構造の下で、韓国民衆による日本の戦争責任追及の声が抑え込まれてきた。だからこそ、冷戦が終焉した1990年代、元従軍慰安婦の人たちをはじめとする韓国、アジアの民衆による日本の戦争責任追及の声が一斉に吹き出てきたのである。

日本国内での靖国問題−戦争責任問題をめぐる議論では、こうした時代認識が圧倒的に希薄だと思うのである。

僕自身は、「戦争後一世代を経て1980年までには戦争の過去はすでに政治家の手を離れ歴史家の手に移っていて、それを意図的に堀り起こして政治問題にしたのは、1982年以降の日本の左翼反体制運動と、謝罪外交に味をしめた中韓。」という認識しか無かったけど、「戦争責任追及の抑え込み」ってホント?

λ. BASTARDのキャラクター名の綴

HAQ BOARDに出て来たので、メモメモ。

ダーク・シュナイダー DARK・SCHNEIDER
ルーシェ・レンレン RUSIE・RENREN
ティア・ノート・ヨーコ TIARA・NORT・YOKO
ジオ・ノート・ソート GEO・NORT・SORT
ガラ GARA
アーシェス・ネイ ARSHES・NEI
カル=ス KALL=SU
アビ ABIGAIL
ラーズ LARZ ULU META=LLICARNA
シーラ SHEERA TUEL META=LLICARNA
シーン SEAN HARRI
カイ KAI HARN
ダイ DI AMON

λ. 借りた本

Tags: 本
[ツッコミを入れる]

2002-08-24

λ. 今日も起きたのはお昼頃。

λ. HAQ Board

が荒れてる。悲しい。

λ. コンパイル猿

というわけで、以下のようなパッチ(#91683)を当てることで、何とかそれっぽく動くようになりました。ウィンドウが表示されてから数秒で暴走するんですが、とりあえずスクリーンショット。 

--- gtk+-2.0.6/gdk/win32/gdkevents-win32.c~	2002-03-06 09:36:08.000000000 +0900
+++ gtk+-2.0.6/gdk/win32/gdkevents-win32.c	2002-08-24 00:38:16.000000000 +0900
@@ -126,7 +126,9 @@
   NULL
 };
 
+#ifdef G_OS_WIN32
 GPollFD event_poll_fd;
+#endif
 
 static GdkWindow *current_window = NULL;
 static gint current_x, current_y;
@@ -317,10 +319,12 @@
   source = g_source_new (&event_funcs, sizeof (GSource));
   g_source_set_priority (source, GDK_PRIORITY_EVENTS);
 
+#ifdef G_OS_WIN32
   event_poll_fd.fd = G_WIN32_MSG_HANDLE;
   event_poll_fd.events = G_IO_IN;
   
   g_source_add_poll (source, &event_poll_fd);
+#endif
   g_source_set_can_recurse (source, TRUE);
   g_source_attach (source, NULL);
 
@@ -3441,11 +3445,15 @@
   
   GDK_THREADS_ENTER ();
 
+#ifdef G_OS_WIN32
   if (event_poll_fd.revents & G_IO_IN)
+#endif
     retval = (_gdk_event_queue_find_first () != NULL)
 	      || PeekMessage (&msg, NULL, 0, 0, PM_NOREMOVE);
+#ifdef G_OS_WIN32
   else
     retval = FALSE;
+#endif
 
   GDK_THREADS_LEAVE ();

PeekMessage()で単純にポーリングするとすごい効率悪そう。Win32でメッセージって普通どうやって扱うんだっけなぁ…… Delphiしか使ったことないので、良く分からなかったり……

[ツッコミを入れる]

2004-08-24

λ. 艦砲射撃!

FLASHのゲーム。ちとはまってしまった。

λ. "A New Method for Functional Arrays", Melissa O'Neill, F. Warren Burton

Syntax Error (2004-08-20) より。配列の外にバージョン管理の情報をつけるのではなく、配列の要素に構造を持たせて、要素レベルでバージョンの管理をする fat element という方法を提案している。「へぇ、こんな方法があるんだ」と感心。計算量はsingle-threadedならO(1)。single-threadedでなくてもアクセスが一様なら、amortizedな計算量でO(1)。それ以外はamortizedな計算量でO(log n)か。結構いいね。

Tags: 論文
[ツッコミを入れる]

2007-08-24

λ. チャーチ・ロッサーの定理の証明

先日は「燃え尽きたので中断する」と書いたが、どうにも気になって頭から離れずモヤモヤしていたら、今日の飲み会中にアイディアを思いついて、結局証明できた。 まだ整理できていない部分が多いが、こんな感じになっている。

【2007-09-09追記】 Frank Pfenning が A Proof of the Church-Rosser Theorem and its Representation in a Logical Framework で LF (の実装のElf)で証明を表現している。後で比較する?

Tags: agda

λ. 同期飲み会

[OTL party]

本日のツッコミ(全4件) [ツッコミを入れる]

ψ oskimura [挫折禁止]

ψ さかい [OTLは「お酒を楽しもうラボ」か何かの略なんですが、どう見ても狙って名前を付けたとしか……]

ψ タナカコウイチロウ [＞飲み会中にアイディアを思いついて すごい。 で、さらに進化形として、勤務中でもバックグラウンドで業務とは関係ない..]

ψ さかい [関係ないことをしている時にアイディアを思いつくというのは良くありますし、当然仕事中に思いつくこともあります (^^;]

2008-08-24

λ. 量子テレポーテーションの行列計算

QMLから量子回路へのコンパイルでは以下のTeleのコンパイル結果の量子ゲートを見てみた。

-- The Teleport algorithm
Tele (a,qb) |- let (b,c) = Epr () 
               in  let f = Bnmeas (a,b)
                   in U (c,f) :: qb;

結果は1qubitの入出力に加えて、2qubitのヒープと2qubitのゴミがある回路だったのだけど、ヒープの初期化と最後の観測を除いた回路本体は3qubitの入出力を持つ回路になっている。この部分はユニタリー変換になっているはずなので、行列に変換してみる。

Prelude QML> s <- readFile "teleport.qml"
Prelude QML> let QAux.OK tele = pTCirc "Tele" s
Prelude QML> QCirc.comp (QTyCirc.circ tele)
OK 
Row/Input Arity = 3,
Column/Output Arity = 3,
([True,True,True],[False,True,True],0.4999999999999999 :+ 0.0)
([True,True,True],[False,True,False],0.4999999999999999 :+ 0.0)
([True,True,True],[False,False,True],(-0.4999999999999999) :+ 0.0)
([True,True,True],[False,False,False],(-0.4999999999999999) :+ 0.0)
([True,True,False],[True,True,True],0.4999999999999999 :+ 0.0)
([True,True,False],[True,True,False],(-0.4999999999999999) :+ 0.0)
([True,True,False],[True,False,True],0.4999999999999999 :+ 0.0)
([True,True,False],[True,False,False],(-0.4999999999999999) :+ 0.0)
([True,False,True],[False,True,True],0.4999999999999999 :+ 0.0)
([True,False,True],[False,True,False],(-0.4999999999999999) :+ 0.0)
([True,False,True],[False,False,True],(-0.4999999999999999) :+ 0.0)
([True,False,True],[False,False,False],0.4999999999999999 :+ 0.0)
([True,False,False],[True,True,True],0.4999999999999999 :+ 0.0)
([True,False,False],[True,True,False],0.4999999999999999 :+ 0.0)
([True,False,False],[True,False,True],0.4999999999999999 :+ 0.0)
([True,False,False],[True,False,False],0.4999999999999999 :+ 0.0)
([False,True,True],[True,True,True],0.4999999999999999 :+ 0.0)
([False,True,True],[True,True,False],0.4999999999999999 :+ 0.0)
([False,True,True],[True,False,True],(-0.4999999999999999) :+ 0.0)
([False,True,True],[True,False,False],(-0.4999999999999999) :+ 0.0)
([False,True,False],[False,True,True],(-0.4999999999999999) :+ 0.0)
([False,True,False],[False,True,False],0.4999999999999999 :+ 0.0)
([False,True,False],[False,False,True],(-0.4999999999999999) :+ 0.0)
([False,True,False],[False,False,False],0.4999999999999999 :+ 0.0)
([False,False,True],[True,True,True],(-0.4999999999999999) :+ 0.0)
([False,False,True],[True,True,False],0.4999999999999999 :+ 0.0)
([False,False,True],[True,False,True],0.4999999999999999 :+ 0.0)
([False,False,True],[True,False,False],(-0.4999999999999999) :+ 0.0)
([False,False,False],[False,True,True],0.4999999999999999 :+ 0.0)
([False,False,False],[False,True,False],0.4999999999999999 :+ 0.0)
([False,False,False],[False,False,True],0.4999999999999999 :+ 0.0)
([False,False,False],[False,False,False],0.4999999999999999 :+ 0.0)

げ、QMLって内部的には横ベクトル使ってるの?　まあ、今更記法を変えるのもアレなので、縦ベクトルに対する線形写像としての行列で書くと、以下のような行列が得られる。

\[U = \frac{1}{2} \left( \begin{array}{rrrrrrrr} 1 & 0 & 1 & 0 & 0 & 1 & 0 & -1 \\ 1 & 0 & -1 & 0 & 0 & -1 & 0 & -1 \\ 1 & 0 & 1 & 0 & 0 & -1 & 0 & 1 \\ 1 & 0 & -1 & 0 & 0 & 1 & 0 & 1 \\ 0 & -1 & 0 & -1 & 1 & 0 & -1 & 0 \\ 0 & 1 & 0 & -1 & 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 & 1 & 0 & -1 & 0 \\ 0 & -1 & 0 & 1 & 1 & 0 & 1 & 0 \\ \end{array} \right)\]

これを (α|0〉 + β|1〉)⊗|00〉 に作用させると、以下のようになり、確かに入力の1qubitはそのまま保たれていて、さらにヒープの2qubitが計算後にはゴミになっていることがわかる。

U ((α|0〉 + β|1〉)⊗|00〉)
= U ((α|000〉 + β|100〉)
= (1/2) (α(|000〉 + |001〉 + |010〉 + |011〉) + β(|100〉 + |101〉 + |110〉 + |111〉))
= (α|0〉 + β|1〉) ⊗ (1/2)(|00〉 + |01〉 + |10〉 + |11〉)

\begin{eqnarray*} \lefteqn{ U (\left(\begin{array}{r}\alpha\\\beta\end{array}\right) \otimes \left(\begin{array}{r}1\\0\\0\\0\end{array}\right)) } \\ &=& \frac{1}{2} \left( \begin{array}{rrrrrrrr} 1 & 0 & 1 & 0 & 0 & 1 & 0 & -1 \\ 1 & 0 & -1 & 0 & 0 & -1 & 0 & -1 \\ 1 & 0 & 1 & 0 & 0 & -1 & 0 & 1 \\ 1 & 0 & -1 & 0 & 0 & 1 & 0 & 1 \\ 0 & -1 & 0 & -1 & 1 & 0 & -1 & 0 \\ 0 & 1 & 0 & -1 & 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 & 1 & 0 & -1 & 0 \\ 0 & -1 & 0 & 1 & 1 & 0 & 1 & 0 \\ \end{array} \right) \left( \begin{array}{r} \alpha \\ 0 \\ 0 \\ 0 \\ \beta \\ 0 \\ 0 \\ 0 \end{array} \right) \\ &=& \frac{1}{2} \left(\begin{array}{r}\alpha\\\alpha\\\alpha\\\alpha\\\beta\\\beta\\\beta\\\beta\end{array}\right) \\ &=& \left(\begin{array}{r}\alpha\\\beta\end{array}\right)\otimes \frac{1}{2}\left(\begin{array}{r}1\\1\\1\\1\end{array}\right) \end{eqnarray*}

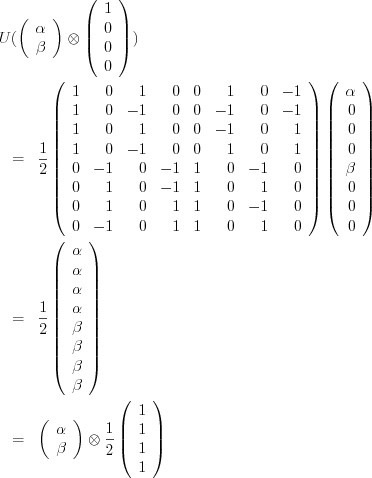
ただ、これだけ見ていると、ヒープとゴミがある分、どうしても恒等写像という感じじゃないんだよなぁ。

こうなってしまうのは、有限次元ヒルベルト空間とユニタリー変換のなす圏を暗黙に考えていたせいで、ユニタリー変換でない「観測」や「ヒープの初期化」を圏の内部では扱えないというのが原因だろう。 QML: A functional quantum programming language によれば、ヒープの初期化を扱うためには射 f : A→B をユニタリー変換からisometryに一般化した圏を考える必要があり、観測を扱うにはさらに射 f : A→B をA上の密度行列からB上の密度行列へのsuperoperatorへと一般化した圏を考える必要があるそうだ。

QMLにはそれらへのコンパイル機能もあるようなので、それもまた今度試してみたい。

Tags: quantum
[ツッコミを入れる]

プロフィール


酒井 政裕

カレンダー

前 2001年
8月		 次
日 月 火 水 木 金 土
1 2 3 4
5 6 7 8 9 10 11
12 13 14 15 16 17 18
19 20 21 22 23 24 25
26 27 28 29 30 31

日記内検索

タグ

本 | logic-programming | tDiary | 英語 | gimp | ruby | cygwin | scheme | gtk | quiz | 流行りもの | 時事 | 映画 | tom | TV | URL | w3m | ネタ | Web | 検索 | 論文 | 圏論 | haskell | javascript | machine-learning | メモ | 向井研 | CPL | 食 | ChannelTheory | linguistics | SemanticWeb | logic | 型理論 | 東方 | continuation | 後で | Topology via Logic | ocaml | modal-logic | theorem-proving | hiki | モデル検査 | 人狼 | programming-contest | agda | probability | quantum | 音楽 | coq | money | Alloy | lifehack | music | maude | プロセス代数 | thinkpad | game | security | linear-programming | optimization | Erlang | iPhone | mac

最近のツッコミ

  1. Lorenzonek (05-21)
  2. さかい (05-07)
  3. mkotha (05-01)
  4. cutsea110 (02-17)
  5. sakai (11-28)
  6. mkotha (11-28)
  7. さかい (07-19)
  8. 山本和彦 (07-19)

最近のトラックバック

この日記と連携する

アンテナ等

日記は現代の病です。読み過ぎ書き過ぎはあなたの健康を害する恐れがあります。くれぐれもご注意下さい。

Generated by tDiary version 4.1.3
Powered by Ruby version 2.2.10-p489