日々の流転

λ. WikiCFP

直江さんが「今までに見つけた中で一番究極なCFP List」 と絶賛していたので試してみるが、便利さはまだよく分からない。 とりあえず、Calls For Papers on Programming Languages のフィードは Google Reader に登録しておこう。

λ. 博士号の取り方。

• 博士号の取り方。- IHARA Note

参考になる(+1)。 そのうち博士号を取ることにするかも知れないので、そのときには参考にしたい。 まだ、「足の裏のご飯粒」とまでは思えないけど、比較的簡単に取れるものなら取っておきたいとは思うしね。

λ. “Metamorphic Programming Extension to Haskell” by Martin Erwig

私が Metamorphism という言葉を初めて聞いたのは、昔の Lambda the Ultimate のGibbons: Metamorphisms and streaming algorithmsという記事だった。 そこでは以下のように紹介されていて、hylomorphismの逆なのかと思っていたが、この論文のはちょっと感じが違うなぁ。

Unfolds generate data structures, and folds consume them. A hylomorphism is a fold after an unfold, generating then consuming a virtual data structure. A metamorphism is the opposite composition, an unfold after a fold; typically,it will convert from one data representation to another.

この論文の動機はADT(Abstract Data Types)に対して fold を定義すること。

(後で書くかも)

λ. Last.fm標準クライアントがiPod対応

Last.fmのWindows用標準クライアント(現在バージョン1.3.2.13b)がいつのまにかiPodに対応していたので、iSprogglerを捨てて、こっちに戻した。 iSprogglerは若干動作が変だったので助かった。 さようなら、iSproggler。

λ. カテ……

圏論勉強会で現在読んでいる“Categories, Types and Structures”について ソフトウェア科学のための論理学 (岩波講座 ソフトウェア科学)(萩谷 昌己) に以下のように書かれていた。カテゴリーの「カテ」までしか書いてないのかよ……

計算機科学者のためのカテゴリー理論の教科書である。計算機科学における応用も含めて、カテゴリーの基礎概念について丁寧に説明している。カテゴリーの「カテ」まで書いてある。残念ながら体裁があまりきれいでない。

λ. “Program-ing Finger Trees in Coq” by Matthieu Sozeau

Finger Tree の実装をダシに、Coqの上に実装されたRusselという言語(?)を紹介している感じ。

しかし、Program-ing Finger Trees In Coq or How To Morph Endo Using Type Theory というスライドのタイトルには笑った。

λ. 型システムを設計する方法論

Type Systems for Resource Bounded Programming and Compilation - Case for Support よりメモ。

The methodology for achieving these goals will be as before: analyse the common patterns of representative case studies, identify appropriate invariants, cast them into an abstract (usually category-theoretic) model, and finally describe the model by a type system.

λ. “State of the Union: Type Inference via Craig Interpolation” by Ranjit Jhala, Rupak Majumdar and Ru-Gang Xu

• <URL:http://www.cse.ucsd.edu/~rjhala/papers/state_of_the_union.html>
• <URL:http://www.springerlink.com/content/h601x44p4379h410/>

<URL:http://fixedpoint.jp/2007/02/10/state_of_the_union.html> より。

Cの共用体は、どの型がいま共用体に格納されているかを覚えていないので、通常タグフィールドと組み合わされて利用される。ので、安全なアクセスであることを検証するために、共用体に対するアクセス時にタグフィールドに関する条件が成り立っていることを静的にチェックすることが考えられる。

条件はアノテーションとして与えることが考えられるけど、ここでは自動的に発見していて面白い。 どうやるかというと、共用体へのアクセスをコントロールフローグラフ(CFG)上で支配するような条件文を集めてきて、各型でアクセスするための条件はdisjointであるはずといった制約を仮定し、Craig Interpolation を使って条件を発見している。 実装は、Cのソースコードの操作やコントロールフローグラフの作成に CIL を、Craig Interpolation に FOCI を利用。

Craig Interpolation が何故こういうことに使えるのか、私はまだ理解できていないので、An interpolating theorem prover を読んでみたいところ。

λ. Twitterにメールから投稿するスクリプト

最近Twitterを始めたyaizawaさんが「なんとたった27行」とか行数自慢(?)していたので、対抗して自分の使っている手抜きスクリプトも晒してみる(^^;

require 'net/http'
Net::HTTP.version_1_2
require 'uri'
require 'tmail'
require 'iconv'

mail = TMail::Mail.parse(STDIN.read)
status = mail.body
status = Iconv.conv('utf-8', mail.charset, status) if mail.charset
status.chomp!

Net::HTTP.start('twitter.com', 80) {|http|
  req = Net::HTTP::Post.new('/statuses/update.json')
  req.basic_auth(ID, PASSWORD)
  req.body = "status=" + URI.escape(status)
  res = http.request(req)
}

λ. 笑顔ボトルキャンペーン

ロッテ・キシリトールのやっている笑顔ボトルキャンペーンに当たった。やったー。

λ. VLAN

Tagged VLAN って、世間ではそんなに使われていないんだろうか。

λ. 『HELLSING (9)』 by 平野 耕太

HELLSING 9 (ヤングキングコミックス)(平野 耕太) を読んだ。 10巻で完結らしいし、最後に向けて盛り上がってきたなあ。

λ. SPASS を試す

SPASS: An Automated Theorem Prover for First-Order Logic with Equality という一階述語論理の定理証明機を見つけたので、ちょっと試してみる。

Smullyan's drinkers' paradox

まずは、こないだ20070828#p02でAgdaで証明を書いた Smullyan's drinkers' paradox を試してみる。

begin_problem(Drinker).

list_of_descriptions.
name({* Smullyan's drinkers' paradox *}).
author({* Masahiro Sakai *}).
status(unsatisfiable).
description({* Smullyan's drinkers' paradox *}).
end_of_list.

list_of_symbols.
predicates[(Drink,1)].
end_of_list.

list_of_formulae(axioms).
end_of_list.

list_of_formulae(conjectures).
formula(exists([x], implies(Drink(x), forall([y], Drink(y))))).
end_of_list.

end_problem.

Webから試せるようになっているので、これを-DocProofオプションと共に与えると何やら証明らしきものが得られるが、読み方が良くわからない。

パースの論理式(Peirce's formula)

命題論理の例として、先日20070814#p01でHaskellで証明したパースの論理式(Peirce's formula)を試してみる。当然何の問題もない。

begin_problem(Peirce).

list_of_descriptions.
name({* Peirce's formula *}).
author({* Masahiro Sakai *}).
status(unsatisfiable).
description({* Peirce's formula *}).
end_of_list.

list_of_symbols.
predicates[(P,0), (Q,0)].
end_of_list.

list_of_formulae(axioms).
end_of_list.

list_of_formulae(conjectures).
formula(implies(implies(implies(P, Q), P), P)).
end_of_list.

end_problem.

様相論理の例 (2007-11-23追記)

命題様相論理の論理式は、「世界」の集合を個体領域とする一階述語論理の論理式に変換することが出来る。 そのため一階述語論理の定理証明器等を様相論理に対して使うことが出来る。 そして、SPASSには様相論理を扱う機能があり*1、変換を自動的に行って証明をしてくれる。

以下の例は、到達可能性関係が反射的であることを仮定して、□A→A を証明する例。 ここでは反射的であることを明示的に公理としているが、オプションで -EMLTheory=2 を指定すれば全ての様相の到達可能性関係が反射的であることは自動的に仮定される。 その方が効率は良いかも。

begin_problem(Reflexivity).

list_of_descriptions.
name({* T from Reflexivity *}).
author({* Masahiro Sakai *}).
status(satisfiable).
description({* T from Reflexivity *}).
end_of_list.

list_of_symbols.
predicates[ (R, 2), (r, 0), (A, 0) ].
translpairs[ (r, R) ]. % r is interpreted as R
end_of_list.

list_of_special_formulae(axioms, eml).
formula( forall([x], R(x, x)) ).
end_of_list.

list_of_special_formulae(conjectures, eml).
prop_formula( implies(box(r, A), A) ). % T
end_of_list.

end_problem.

λ. “A new view of guards” by Simon Peyton Jones

を読んだ。 へぇ、パターンガードってこういうものだったのね。

λ. HaskellのDynamicはあまり使えない

現在のHaskell(GHC)のDynamicは言語的なサポートがないため、Cleanのそれに比べると記述能力の点で非常に貧弱で、ユーザー定義の型を例外として投げるとかそのくらいの用途にしか使えない。

例えば、dynFst (toDyn (a,b)) = Just (toDyn a) を満たすような関数 dynFst :: Dynamic → Maybe Dynamic すら a, b の型を予め特定の型に決めないと記述することが出来ない。fromDyn等によって値を取り出す際には、Typeableのインスタンスとして型を取り出すわけだけど、これはTypeRepで型を指定していることに等しく、TypeRepは型変数を含まないため。 言語拡張にしてしまえば、このような関数を(安全に)記述できるようにすることはそう難しくはないはずなんだけど。

λ. UNIQLOCK

今更ながらUNIQLOCKにはまる。 これはいいなぁ。かわいいなぁ。

λ. “Why it's nice to be quoted: quasiquoting for haskell” by Geoffrey Mainland

• <URL:http://portal.acm.org/citation.cfm?id=1291211>
• <URL:http://www.eecs.harvard.edu/~mainland/ghc-quasiquoting/>

を読んだ。 Haskelに quasi quote を導入する話。 これば便利そう。

λ. RHG読書会::東京 Practical Common Lisp

λ. Right Brain v Left Brain

某氏の日記より。

自分の場合、最初は時計回りにしか見えなくて、「これが反時計回りに見えるなんてなんかおかしいんじゃない?」とか思ったんだけど、足元と影を見ていたら回転が切り替わった。 確かに、どちらにも見ることが出来るんだけど、切り替わる瞬間がなんだか不思議な感じで面白い。でも酔いそうだ。

λ. OperaのiframeのcontentDocumentが変

MAD PEOPLE 用の発言ポップアップスクリプト が最近のOpera(Opera 9.21)で動かなくなっていたので調べたら、iframeの振る舞いが変わってしまっていた。 iframeからcontentDocumentでHTMLDocumentオブジェクトを取得し、その後そのiframeをremoveChildしたら、取得したオブジェクトがただのObjectになってしまって、HTMLDocumentとして操作できなくなってしまう。 昔のOperaはこんなことなかったんだけどなぁ。バグ?

ぐぐってみると、<URL:http://d.hatena.ne.jp/quaa/20070807#p1> に同じことが書いてあって、iframe.contentDocument.documentElement.ownerDocument として取得しておけば回避出来るようだ。

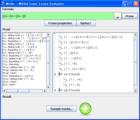
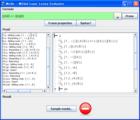
λ. Molle (MOdal Logic Loony Evaluator)

最近様相論理の定理証明器を少し探していて見つけた、タブローによる証明器。 Javaで書かれていて簡単に試せる。 ただ、複数の様相を扱えず、またKでの証明しか扱えないっぽい。

スクリーンショット

□(A→B)→□A→□B を証明させた場合

□(A∨B)→□A∨□B を証明させた場合

□(A∨B)→□A∨□B の反例のクリプキ構造

λ. SPASSで知識の論理を使って論理パズルを解く?

最近、論理パズルを解くのに使える様相論理のツールはないかと探していたのだけど、SPASSは結構使えそうな感じなので、SPASSで知識の論理を使って論理パズルを解いてみようと思った。

題材は、以前に「トランプの和と積のパズル」と様相論理で形式化したトランプの和と積のパズルに挑戦しようと思ったのだけど、いきなり挑戦するにはちょっと複雑すぎるので、もう少し簡単な問題にする。 何にしようか少し迷ったが、情報科学における論理 (情報数学セミナー)(小野 寛晰) の p.187 「論理パズルと知識の論理」で紹介されている、赤いぼうし (美しい数学 (5))(野崎 昭弘/安野 光雅) の話を使うことにした。この問題を非常に簡単に説明すると以下のようになる。

AさんとBさんがいて、少なくとも一人は赤い帽子を被っていて、赤い帽子を被っていない人は白い帽子を被っている。 ただし、二人とも他人の帽子の色は分かるが、自分の被っている帽子の色は分からない。 そして、Aさんが「自分の帽子の色が分からない」と発言した。 このとき、Bさんの被っている帽子の色は何か?　そして、Bさんは自分の被っている帽子の色が分かるか?

ちょっと考えると、Bさんの被っている帽子の色が赤で、そしてBさんもそのことを知ることが出来ることがわかる。これをSPASSで表現すると以下のようになる。 ここでコマンドラインオプションの -EMLTheory=7 は全ての様相がS5様相であること、すなわち到達可能性関係が同値関係であることを指定している。

% SPASS -EMLTheory=7 -DocProof RedHat.dfg
begin_problem(RedHat).

list_of_descriptions.
  name({* Red Hat *}).
  author({* Masahiro Sakai *}).
  status(unsatisfiable).
  description({* 「赤いぼうし」の問題 *}).
end_of_list.

list_of_symbols.
  predicates[ (a,0) % Aさんの帽子が赤
            , (b,0) % Bさんの帽子が赤
            , (Ka,0), (Ra,2) % Aさんが知っているという様相
            , (Kb,0), (Rb,2) % Bさんが知っているという様相
            , (E,0),  (Re,2) % 二人とも知っているという様相
            , (C,0),  (Rc,2) % 共通知識であるという様相
            ].
  translpairs[ (Ka,Ra), (Kb,Rb), (E,Re), (C,Rc) ].
end_of_list.

list_of_special_formulae(axioms, eml).
  % [E]P <-> [Ka]P∧[Kb]P
  formula( forall([x,y], equiv(Re(x,y), or(Ra(x,y), Rb(x,y)))) ).
  % [C]P <-> [E][C]P
  formula( forall([x,y], equiv(Rc(x,y),
                               exists([z], and(Re(x,z), Rc(z,y))))) ).

  % どちらかの帽子は赤である
  prop_formula( box(C, or(a, b)) ).  
  % AさんはBさんの帽子の色を知っている
  prop_formula( box(C, or(box(Ka, b), box(Ka, not(b)))) ).
  % BさんはAさんの帽子の色を知っている
  prop_formula( box(C, or(box(Kb, a), box(Kb, not(a)))) ).

  % Aさんは自分の帽子の色が分からない
  prop_formula( box(C, not(box(Ka, a))) ).
  prop_formula( box(C, not(box(Ka, not(a)))) ).
end_of_list.

list_of_special_formulae(conjectures, eml).
  % Bさんは「自分の帽子の色は赤である」ことを知っている
  prop_formula( box(Kb,b) ).
end_of_list.

end_problem.

これをSPASSに証明させると証明に成功し、この推論が正しいことが分かる。 ただし、box(Kb,not(b)) を証明させようとすると止まらなくなるようなので、推論が正しいことを確認することは出来ても、問題を解くのには使えないかも。

【2007-12-10追記】 上記の定義には問題があることに気がついた(止まらない原因に関係があるかは不明)。 [C]P は F(X) = [E](P×X) の単なる不動点ではなく最大不動点である必要があるようだ。 これは一階述語論理に翻訳すると [C] の到達可能性関係 Rc が [E] の到達可能性関係 Re の推移閉包(transitive closure)になっていることに対応するのだが、これが表現できていない。 色々考えたが、どうも推移閉包は一階述語論理では表現できないようだ。

【2007-12-16追記】 上記では公理には各前提条件に共通知識の様相をつけていたけど、これは不要だった。 何故ならば、共通知識の様相付きの論理式から導出できることは全部、様相の付いてない論理式からも「必然化(necessitation)」を使って導出できるため。 これは Mechanizing common knowledge logic using COQ (c.f. 20071217#p01)を読んで知ったのだけど、何故こんな簡単な事を自分気付けなかったのだろう……orz　あと、共通知識の様相を使わなくした場合でも停まらないのは変わらなかったので、共通知識の様相の形式化は停まらないのには関係なかった。

λ. DCG で a^n b^n c^n (n > 0) という言語を表現できるか?

数日前に水島さんがTwitterで「ところで、 DCG で a^n b^n c^n という言語を表現できます？ (PEG で表現できて CFG で表現できない言語の例 )」と書いていた。 その後の議論は追いかけていないけど、素性の一致を書ける(cf. Haskellでパーサを書く時に面倒な点)くらいだから、そんなのは自明に表現できる。

s --> {N=s(_)}, as(N), bs(N), cs(N).

as(z) --> [].
as(s(N)) --> [a], as(N).

bs(z) --> [].
bs(s(N)) --> [b], bs(N).

cs(z) --> [].
cs(s(N)) --> [c], cs(N).

使用例は以下のような感じ。

?- s([],[]).
No
?- s([a,b,c],[]).
Yes
?- s([a,a,b,c],[]).
No
?- s([a,a,b,b,c,c],[]).
Yes
?- s(X,[]).
X = [a, b, c] ;
X = [a, a, b, b, c, c] ;
X = [a, a, a, b, b, b, c, c, c]
Yes
?-

PrologやDCGについて興味のある方は、向井先生と尾崎先生の「論理プログラミング」講義資料(2004年度)などを参照すると良いかもしれません。

λ. 東方風神録、霊夢TypeBでノーマルクリア

霊夢TypeBでのノーマル初クリア(th10_03.rpy)。 ステージ6は集中力切れた。 けど、マウンテンオブフェイスは初めてとれた。

東方風神録 リプレイファイル情報
Version 1.00a
Name hiro    
Date 07/11/25 15:19
Chara ReimuB 
Rank Normal 
Stage All Clear
Score 38100982
Slow Rate 3.65

λ. PEG意見交換会

PEG意見交換会のUstream.tvでのストリーミングを見たら、ちょうど稲葉さんの発表の途中だった。

「A ← ‘a’ A ‘a’/ ‘a’」が「aaaaa」にマッチしないって、思ってたよりもPEGってだいぶ非直観的なんだな。 あと、ちょっと気になったのは、発表資料に「理論的に『PEGにマッチする例を完全に列挙』は不可能」と書いてあったところ。全ての文脈依存言語は帰納的(recursive)で当然帰納的可算(recursively enumerable)なので、これはつまりPEGでは文脈依存言語でない言語を表現できるということなのだろうか。

【追記】 色々と勘違いしてた。いくらなんでも構文解析は決定可能だろうから、PEGの表す言語は帰納的で、したがって帰納的可算なので、マッチする例を列挙することは可能。それと、文脈依存言語⊂帰納的言語なので、PEGが文脈依存でない言語を表せるかどうかはまた別の問題。

λ. 「ガン検診」問題でPRISMを試す

一階述語論理と確率を統合したツールとしてPRISMというものがある。

前々から存在は知っていたけど、最近渕一博記念コロキウム『論理と推論技術：四半世紀の展開』(20071020)の「記号的統計モデリングの世界を探る」(佐藤泰介)という発表を聴き、また「コンピュータソフトウェア」(Vol. 24 No. 4 Oct. 2007)に載っていた「PRISM: 確率モデリングのための論理プログラミング処理系」(亀谷由隆, 佐藤泰介, 周能法, 泉祐介, 岩崎達也)を読んで面白かったので、ちょっと試してみようと思った。

まずは非常に簡単な例として、ベイズのルールの例としてよく出てくるガン検診の例を試してみる。 以下は、昔受講した井庭先生の「探索的モデリング」(2004年度)の第3回「ベイズ確率 reloaded」より引用。

あるガン検診の方法は、ガンの人は0.95の確率でガン陽性と診断され、健康な人がガン陽性と誤診される確率は0.05だとする。(つまり、どちらにしても的中率95%)　ガンにかかる確率を0.005とする。この検査の結果、「ガン陽性である」という診断がでたら、自分のガンの可能性をどの程度と疑うべきだろうか?

これをPRISMでモデル化すると以下のようになる。

% cancer.psm
target(p/2). % 確率事象を表現する述語の宣言
values(cancer, [t, f]). % 確率変数cancerのとる値
values(test(_), [positive, negative]). % 確率変数test(_)のとる値

p(CANCER, RESULT) :-
  msw(cancer, CANCER),       % CANCERは確率変数cancerの値
  msw(test(CANCER), RESULT). % RESULTは確率変数test(CANCER)の値

% 確率分布の設定
:- set_sw(cancer,  [0.005, 0.995]).
:- set_sw(test(t), [0.95, 0.05]).
:- set_sw(test(f), [0.05, 0.95]).

これをPRISMに読み込ませて、「ガン陽性である」という診断が出たときに実際にガンである確率(事後確率)を計算してみる。

[sakai@localhost ~]% prism
PRISM 1.11.1, Sato Lab, TITECH, All Rights Reserved. Nov 2007
B-Prolog Version 7.0, All rights reserved, (C) Afany Software 1994-2007.

Type 'prism_help' for usage.
| ?- prism(cancer).
prism(cancer).

compiled in 0 milliseconds
loading::cancer.psm.out

yes
| ?- chindsight_agg(p(_, positive), p(query, _)).
chindsight_agg(p(_, positive), p(query, _)).

conditional hindsight probabilities:
  p(f,*): 0.912844036697248
  p(t,*): 0.087155963302752

yes
| ?-

事後確率が計算され、実際にガンである確率が約9%、実際にはガンでない確率が約91%という結果が得られる。 つまり、このモデルだと、ガンと診断されても実際にはガンでない可能性の方が遥かに高いわけですね。

うん、確かに非常に手軽に色々出来そうだ。 というか、確率推論や確率の学習を行うだけなら、探索的モデリングの授業で使ったBayonetよりもずっと手軽そうだ。 グラフ構造を推定したりしたいような場合には使えないとは思うけど。

λ. Re: EXPTIME とか PSPACE とか

あろはさんのホワット・ア・ワンダフル・ワールド 真面目に計算の複雑性の理論を勉強してこなかったツケがより。

非常にわかりやすくて、勉強になる。交替性有限オートマトン(Alternating Finite Automata, AFA)にはお世話になっているけど、交替性チューリング機械なんてのも存在して、計算量理論で意味を持っていたとは。

ちなみに、SFCでは [Chandra-Kozen-Stockmeyer] を教えてくれるどころか、計算量理論を扱う授業自体が無かった…… orz

λ. CSLI Lecture Notes online and free

いまさらだけど <URL:http://lambda-the-ultimate.org/node/2532> より。 CSLI Lecture Notes がオンラインでフリーで読めるようになったらしい。 Aczel の Non-well-founded Sets とか色々あるな。 すごいなぁ。

λ. “Context Threading: A flexible and efficient dispatch technique for virtual machine interpreters” by Marc Berndl, Benjamin Vitale, Mathew Zaleski and Angela Demke Brown

を読んだ。 <URL:http://www.atdot.net/~ko1/diary/200711.html#d23> より。

λ. SNS型英語学習サイト iKnow!

iKnow! は語学を学ぶ人のための、パーソナル学習アプリケーションを搭載したコミュニティーサイトです。脳科学に基づいて開発されたラーニング・エンジンが、あなたの学習パフォーマンスをすべてトラッキング。　最適な学習プランを自動的に提供するという画期的、かつ効果的な方法で、英語を学習していきます。

とおる。さんのところより。 早速登録してみた(http://www.iknow.co.jp/user/sakai)けど、結構良さそう。 ただ、問題なのは続くかどうかなんだよな。 僕の英語学習で続いてるのはESLPodだけで、他は英語漬けも単語力もNPRも英語日記もぜーんぶ続いてないからなぁ。

λ. 某銀行の口座を解約

今日は会社がお休みだったので、ここ数年使っていなかった某銀行の口座を解約してきた。月末だったので30分以上かかった。

λ. SFCの紅葉

その後ふらふらっとSFCへ。 木々が紅葉していて綺麗だった。

4月にメディアセンターの図書利用券を申し込んだが、仮図書利用券と引き換えに図書利用券を受け取る。ただ、正直SFCでだけ入館&貸し出し出来るやつよりも、慶應の全メディアセンターで入館できるやつにした方が良かったな。なかなか定期的に来るのは難しいから、なかなか借りにくいんだよな。

萩野・服部研の研究室を覗いたら誰も居なかったので、古川研の研究室に少しお邪魔しにいき、それから向井先生のところへ。 今期の研究会では「インフレーションからビッグバンまで」と「伊藤 清の『確率過程』を読む」というのをやっていて、今日は後者の方の研究会だった。 丁度、Radon-Nikodym theorem というのをやっていたが、僕は測度論はさっぱりなので、さっぱりわからず。 なお、このラドンさんの名前を冠したラドン変換というのがあり、その逆変換がCT(Computed tomography)で使われているそうな。

それと、もう片方の研究会に関係してシュレーディンガーのジレンマと夢―確率過程と波動力学(長沢 正雄)という本を紹介していただいた。確率過程論をベースにした、量子論の非標準的な解釈だとか。

• 森北出版｜シュレーディンガーのジレンマと夢 - PDFによる見本と、森毅氏と川久保達之氏の推薦文あり

そのほかにも色々話す。非文とかdisplay logicとかビザンチン将軍問題 (Byzantine fault tolerance)とか。