日々の流転

λ. 寒空の下のキャンパス

マクロ経済の補講で学校へ行った。どうでも良いことではあるけど、公定歩合はマルクス経済学では手形の再割引率であるとされていたらしい。こういうのって面白くって好き。それから、王先生の研究室を見学して、ついでに春学期の「マクロ経済Ⅱ」のOHP(を印刷したやつ)を貰った。そういえば、今日はAmayaの開発者の人がSFCに来ると聞いてたけど、時間と場所を聞くのを忘れてた。しまったなぁ。Amayaのソースには文句を言わなきゃ気がすまないのにー　と最初は思ったが、僕が文句を垂れたからといって直ぐに状況が改善するとも思えないし、時間と場所を誰かに訊いてまで会いに行くという行為がしだいにアホらしくなってきたので、適当に時間を潰してから帰る事にする。

λ. 情報通信セキュリティ論

拡大体GF(2^m)上の演算が理解できてなかったんだけど、何度か読み直してやっと少しずつ分かってきた。これなら明日提出の宿題も何とかなるかな。つーか、ガロアすげーよ

λ. 論理的月曜日

Happy Monday 法の影響で今日は月曜日の時間割。でも、所詮ローカル・ルールなので、学外での予定とコンフリクトしている教員が多そう。実際、僕の取ってる授業は2限のコンパイラ構成論以外ぜんぶ休講ですよ。あー、阿保らしー

λ. コンパイラ構成論

属性文法が0型文法と等価だというのが、いまいちピンと来ない。

λ. 予定利率下げへ法改正・金融庁方針

.

λ. 蝶ネクタイ理論

23日の日記間リンクの話に関係して、Web全体の構造が蝶ネクタイ状になっているとの研究を加藤さんに教えてもらった。

• Graph structure in the web
• http://www.research.ibm.com/resources/news/20000511_bowtie.shtml
• http://www.watch.impress.co.jp/internet/www/article/2000/0512/bowtie.htm

λ. エニックスとスクウェア「来年４月に合併」

あの財務体質じゃねぇというのは置いておいて、FFやドラクエよりもアクトレイザー3を出してくだせぇ。

λ. REXML

ふとXMLで書かれたファイルを扱いたくなってREXMLを試してみたけど、いまいち使いづらい。例えば、eachに引数を渡す使い方があるけど、これだとEnumerableの機能が使えないし……

λ. URI

URI::Genericをハッシュのキーに使おうとしてはまる。hashもeql?も定義されてないのね……

λ. 読書

『かってに改蔵 18』

久米田 康冶 [著]

λ. ボーリング

katoken, wisteria, jn, sakaiでボーリングへ。katokenさん強いっす。スコア

λ. 世界制服もとい世界征服

世界征服の前に立ちふさがる最凶の問題はどうやら久野君らしい。敵に回すのは恐ろし過ぎるし、かといって懐柔しても寝首をかかれそうとのこと。

λ. Intuitionistic type theory

9/27に借りてから随分経ってしまったけど、ようやく読了。Wellorderingsの章を除けば大体理解できたと思う。身に付いているかは別だけど。(苦笑)

Wellorderingsに関してはこんど向井先生に訊いてみよう。

λ. エスプレッソ

『「エスプレッソ」って最後の「ッソ」を省略すると「コスプレ」みたいだよね』と某氏のお言葉。

λ. 「ガン検診」問題でPRISMを試す

一階述語論理と確率を統合したツールとしてPRISMというものがある。

前々から存在は知っていたけど、最近渕一博記念コロキウム『論理と推論技術：四半世紀の展開』(20071020)の「記号的統計モデリングの世界を探る」(佐藤泰介)という発表を聴き、また「コンピュータソフトウェア」(Vol. 24 No. 4 Oct. 2007)に載っていた「PRISM: 確率モデリングのための論理プログラミング処理系」(亀谷由隆, 佐藤泰介, 周能法, 泉祐介, 岩崎達也)を読んで面白かったので、ちょっと試してみようと思った。

まずは非常に簡単な例として、ベイズのルールの例としてよく出てくるガン検診の例を試してみる。 以下は、昔受講した井庭先生の「探索的モデリング」(2004年度)の第3回「ベイズ確率 reloaded」より引用。

あるガン検診の方法は、ガンの人は0.95の確率でガン陽性と診断され、健康な人がガン陽性と誤診される確率は0.05だとする。(つまり、どちらにしても的中率95%)　ガンにかかる確率を0.005とする。この検査の結果、「ガン陽性である」という診断がでたら、自分のガンの可能性をどの程度と疑うべきだろうか?

これをPRISMでモデル化すると以下のようになる。

% cancer.psm
target(p/2). % 確率事象を表現する述語の宣言
values(cancer, [t, f]). % 確率変数cancerのとる値
values(test(_), [positive, negative]). % 確率変数test(_)のとる値

p(CANCER, RESULT) :-
  msw(cancer, CANCER),       % CANCERは確率変数cancerの値
  msw(test(CANCER), RESULT). % RESULTは確率変数test(CANCER)の値

% 確率分布の設定
:- set_sw(cancer,  [0.005, 0.995]).
:- set_sw(test(t), [0.95, 0.05]).
:- set_sw(test(f), [0.05, 0.95]).

これをPRISMに読み込ませて、「ガン陽性である」という診断が出たときに実際にガンである確率(事後確率)を計算してみる。

[sakai@localhost ~]% prism
PRISM 1.11.1, Sato Lab, TITECH, All Rights Reserved. Nov 2007
B-Prolog Version 7.0, All rights reserved, (C) Afany Software 1994-2007.

Type 'prism_help' for usage.
| ?- prism(cancer).
prism(cancer).

compiled in 0 milliseconds
loading::cancer.psm.out

yes
| ?- chindsight_agg(p(_, positive), p(query, _)).
chindsight_agg(p(_, positive), p(query, _)).

conditional hindsight probabilities:
  p(f,*): 0.912844036697248
  p(t,*): 0.087155963302752

yes
| ?-

事後確率が計算され、実際にガンである確率が約9%、実際にはガンでない確率が約91%という結果が得られる。 つまり、このモデルだと、ガンと診断されても実際にはガンでない可能性の方が遥かに高いわけですね。

うん、確かに非常に手軽に色々出来そうだ。 というか、確率推論や確率の学習を行うだけなら、探索的モデリングの授業で使ったBayonetよりもずっと手軽そうだ。 グラフ構造を推定したりしたいような場合には使えないとは思うけど。

λ. Re: EXPTIME とか PSPACE とか

あろはさんのホワット・ア・ワンダフル・ワールド 真面目に計算の複雑性の理論を勉強してこなかったツケがより。

非常にわかりやすくて、勉強になる。交替性有限オートマトン(Alternating Finite Automata, AFA)にはお世話になっているけど、交替性チューリング機械なんてのも存在して、計算量理論で意味を持っていたとは。

ちなみに、SFCでは [Chandra-Kozen-Stockmeyer] を教えてくれるどころか、計算量理論を扱う授業自体が無かった…… orz

λ. 舎利禮文 【初音ミク×M＠STER_fonts Pv】

このセンスは凄いな。

λ. 今日も泳いできた

今日も帰りに泳いできた。 だんだん、1km泳いでもそんなにバテないようになってきた。

λ. 祖父の葬儀

(後で書く)

λ. 自動微分を使って線形回帰をしてみる

Conal Elliott の Beautiful differentiation の論文を読んだ話 の続き。 自動微分の機械学習系での応用は分かるという話で、せっかくなので一番簡単な線形回帰でも使って試してみることに。

データ例

例としては、Rでお馴染みのgaltonのデータを使う。 これは、リンク先にも書いてあるけど、Galtonさんが1885に両親の身長と子供の身長の関係を分析したデータセットで、928サンプルが含まれている。RのUsingRパッケージに含まれているので、これをRで以下のようにして、galton.csvに保存しておく。

> install.packages("UsingR")
> library(UsingR)
> data(galton)
> write.csv(galton, "galton.csv", row.names = FALSE)

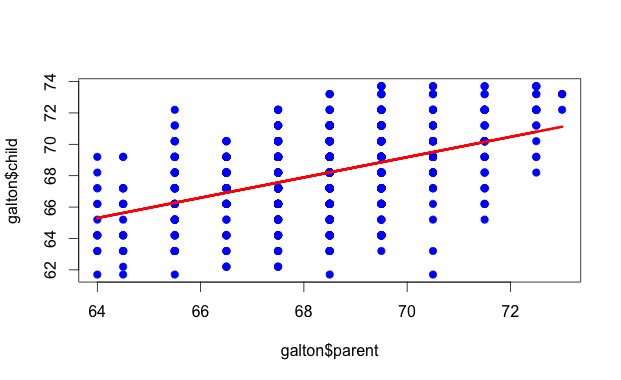
せっかくなので、Rで線形回帰をして散布図上にプロットしておく。

> lm <- lm(galton$child ~ galton$parent)
> summary(lm)

Call:
lm(formula = galton$child ~ galton$parent)

Residuals:
    Min      1Q  Median      3Q     Max 
-7.8050 -1.3661  0.0487  1.6339  5.9264 

Coefficients:
              Estimate Std. Error t value Pr(>|t|)    
(Intercept)   23.94153    2.81088   8.517   <2e-16 ***
galton$parent  0.64629    0.04114  15.711   <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 

Residual standard error: 2.239 on 926 degrees of freedom
Multiple R-squared: 0.2105,	Adjusted R-squared: 0.2096 
F-statistic: 246.8 on 1 and 926 DF,  p-value: < 2.2e-16

> plot(galton$parent, galton$child, pch=19, col="blue")
> lines(galton$parent, lm$fitted, col="red", lwd=3)

自動微分のコード

Conal Elliott のコードを使おうかと思ったけれど、Hackageにekmettプロダクトのadパッケージがあったので、それを使うことに。バージョンは3.4を使う。 そういえば、先日開催されていたekmett勉強会でも、@nebutalabという方がadの紹介をしていた。

最急降下法

で、grad関数で自動微分して勾配を求めて、それを使って最急降下法するコードを自分で書こうと思ったら、ちょうど都合の良いことにgradientDescentという関数が用意されていた。 なので、これを使うことにして書いてみたのが以下のコード。 gradientDescentには普通に目的関数costと初期値を引き渡しているだけで、勾配を計算するための関数などを全く引き渡していないことに注目。

-- Galton.hs
module Main where

import Control.Monad
import Numeric.AD
import Text.Printf
import qualified Text.CSV as CSV

main :: IO ()
main = do
  Right csv <- CSV.parseCSVFromFile "galton.csv"
  let samples :: [(Double, Double)]
      samples = [(read parent, read child) | [child,parent] <- tail csv]      
      -- hypothesis
      h [theta0,theta1] x = theta0 + theta1*x
      -- cost function
      cost theta = mse [(realToFrac x, realToFrac y) | (x,y) <- samples] (h theta)
  forM_ (zip [(0::Int)..] (gradientDescent cost [0,0])) $ \(n,theta) -> do
    printf "[%d] cost = %f, theta = %s\n" n (cost theta :: Double) (show theta)

-- mean squared error
mse :: Fractional y => [(x,y)] -> (x -> y) -> y
mse samples h = sum [(h x - y)^(2::Int) | (x,y) <- samples] / fromIntegral (length samples)

実行結果

それで、コンパイルして実行してみると……

[0] cost = 3156.057306315988, theta = [2.6597058526401096e-2,1.8176025390625015]
[1] cost = 2146.158122210389, theta = [4.6848451721258726e-3,0.3193588373256373]
[2] cost = 1459.9671459993929, theta = [2.2758658044906822e-2,1.5543558052476183]
[3] cost = 993.724511817967, theta = [7.872126807824226e-3,0.5363518751316139]
[4] cost = 676.9290401789791, theta = [2.0154694031410444e-2,1.3754888484523264]
[5] cost = 461.6776592383078, theta = [1.0041866689573948e-2,0.6837909525010937]
[6] cost = 315.42191649062323, theta = [1.8389486179011837e-2,1.2539549823963831]
[7] cost = 216.0462832295627, theta = [1.1520222735584755e-2,0.783970560056418]
[8] cost = 148.52403553080242, theta = [1.719418363575862e-2,1.1713769350191798]
[9] cost = 102.64504299700745, theta = [1.252880777988588e-2,0.8520390200495115]
…
[100] cost = 5.391540483678139, theta = [1.5252813280501425e-2,0.9963219150471427]
[101] cost = 5.391540272870362, theta = [1.5259169016306468e-2,0.9963197390947276]
[102] cost = 5.391540062688162, theta = [1.5265580330093717e-2,0.9963213622860531]
[103] cost = 5.3915398529310075, theta = [1.5271945828031475e-2,0.9963198538562846]
[104] cost = 5.391539446704301, theta = [1.5284752349382588e-2,0.996321999765866]
…
[1000] cost = 5.3913214546153885, theta = [2.195100305728909e-2,0.9962239448356897]
[1001] cost = 5.39132107512034, theta = [2.19637098242177e-2,0.9962195158083134]
[1002] cost = 5.391320924102971, theta = [2.1976643022454955e-2,0.996230564935548]
[1003] cost = 5.391320615754077, theta = [2.198280974693417e-2,0.9962155918323486]
[1004] cost = 5.391320339333709, theta = [2.1989373588151114e-2,0.9962277637190161]
…
[10000] cost = 5.389137897180453, theta = [8.88298535971496e-2,0.9952457730583962]
[10001] cost = 5.38913768668423, theta = [8.8836182876215e-2,0.9952431313378857]
[10002] cost = 5.389137477124735, theta = [8.884258017163454e-2,0.995245138984378]
[10003] cost = 5.389137268201876, theta = [8.884892139830691e-2,0.995243314173662]
[10004] cost = 5.389136870256361, theta = [8.886169628000305e-2,0.9952459827149522]

全然収束しない。収束遅すぎだろ。めげずにさらに放置してると……

[100000] cost = 5.367962167905593, theta = [0.7474196350908293,0.9856182795949244]
[100001] cost = 5.367961856713982, theta = [0.7474255920526732,0.9856022065240108]
[100002] cost = 5.367961582358961, theta = [0.7474319755635072,0.9856152902779793]
[100003] cost = 5.367961333033166, theta = [0.747438007468459,0.9856043401613668]
[100004] cost = 5.367961100713857, theta = [0.7474443291979176,0.9856132010817849]
…
[1000000] cost = 5.210315054542271, theta = [6.411550087218479,0.9027479380474824]
[1000001] cost = 5.210314936517216, theta = [6.411554713147153,0.9027442449249086]
[1000002] cost = 5.210314820386824, theta = [6.411559435811994,0.9027471642783936]
[1000003] cost = 5.210314705543812, theta = [6.411564078735267,0.9027446329906037]
[1000004] cost = 5.210314591575562, theta = [6.411568787386962,0.9027465946477329]
…
[5000000] cost = 5.0177281352658305, theta = [18.890815946868038,0.7201815311956332]
[5000001] cost = 5.017728123133143, theta = [18.890817258298373,0.7201790053001258]
[5000002] cost = 5.017728111906337, theta = [18.89081863661461,0.720181051408368]
[5000003] cost = 5.017728101294881, theta = [18.89081995979637,0.7201793288296293]
[5000004] cost = 5.01772809110162, theta = [18.890821328424636,0.7201807127666369]
…
[10000000] cost = 5.001070611475556, theta = [22.875383075131683,0.6618880826205324]
[10000001] cost = 5.00107061095209, theta = [22.87538335250446,0.6618875866914469]
[10000002] cost = 5.001070610463426, theta = [22.875383643001708,0.6618879878893927]
[10000003] cost = 5.001070609998513, theta = [22.875383922680363,0.6618876495886096]
[10000004] cost = 5.001070609549686, theta = [22.87538421127661,0.6618879208540909]

まだかかるのかよ……

[15000000] cost = 5.000328380487849, theta = [23.716478910924902,0.6495830291863548]
[15000001] cost = 5.0003283804652, theta = [23.71647896958202,0.6495829318117019]
[15000002] cost = 5.000328380443848, theta = [23.71647903081446,0.6495830104741416]
[15000003] cost = 5.000328380423461, theta = [23.716479089924043,0.6495829440298111]
[15000004] cost = 5.000328380403642, theta = [23.71647915078346,0.649582997196493]
…
[20000000] cost = 5.0002953079344685, theta = [23.894024471635685,0.6469855785633368]
[20000001] cost = 5.000295307933508, theta = [23.894024484038532,0.64698555944479]
[20000002] cost = 5.000295307932569, theta = [23.89402449694667,0.6469855748657359]
[20000003] cost = 5.0002953079316805, theta = [23.894024509438292,0.6469855618158963]
[20000004] cost = 5.000295307930787, theta = [23.89402452227324,0.6469855722344278]
…
[22987995] cost = 5.000294005873883, theta = [23.922778217862263,0.6465649143875803]
[22987996] cost = 5.000294005873744, theta = [23.922778220364872,0.6465649143543949]
[22987997] cost = 5.000294005873735, theta = [23.922778220366094,0.6465649143543771]
[22987998] cost = 5.000294005873733, theta = [23.922778220367316,0.6465649143543594]
[22987999] cost = 5.000294005873733, theta = [23.922778220367316,0.6465649143543594]
[22988000] cost = 5.000294005873733, theta = [23.922778220367316,0.6465649143543594]

やった！　収束した！

Rだと一瞬だったところ、1.5日くらいかかったし、Rで計算した theta0=23.94153, theta1=0.64629 とはちょっとずれてはいるけれど。

感想

Courseraの Machine Learning のコースで、最急降下法で線形回帰を実装したときは1000ステップくらいで収束してたので、これもそれくらいで収束するかと思ってたんだけれど、こんなにかかるとは以外だった。 gradientDescent関数(ソース)の実装に何か問題があるのか、それともそもそも素朴な最急降下法には荷の重い問題だったのか分からんけれど、2パラメータのこの程度の問題でこれは流石に酷い。

本当はこの後は、ロジスティック回帰とニューラルネットの例も何かやってみようかと思ってたのだけれど、その前にそっちを何とかしないといけないかも。 Machine Learning のコースでも最初は簡単な再急降下法を自前で実装させていたけれど、その後は最適化は予め用意してある実装(fmincg.m)を使うようになってたからなぁ。 まあ、時間かかりすぎて疲れたので、また今度。

【追記】頂いたコメンドなど

これは中で使ってる勾配法のステップ設定が狂っている感．このデータなら単純な勾配法でもここまで収束遅くはないと思われる．

— Takanori MAEHARA (@tmaehara) November 27, 2013

目的関数値の減少量はステップ幅と同じくらいのオーダーのはずだから，ステップ幅のスケジューリングが急すぎるとかかしらん……．

— Takanori MAEHARA (@tmaehara) November 27, 2013

【追記】 解決策

• conjugated gradient descent などのより賢い最適化手法を使う → nonlinear-optimizationパッケージで遊ぶ (ヒビルテ 2013-11-28)
• データのスケーリング → コメント欄参照
• 勾配法のステップ設定 → ？