日々の流転

λ. ぐだぐだ。

λ. 夢

美人のお姉さんの官僚さんに、貿易が為替レートに与える影響について頑張って説明したのに、全然理解してくれないという夢を見ました。手を変え品を変え説明したんだけど、彼女は「為替レートが貿易に影響を与えるのであって、それでは因果関係が逆だ」と固く信じていて、僕の説明を全然受け入れてくれませんでした。説明していて疲れました。まる。

λ. Linux

2.5ではプロセスごとにファイルシステムの名前空間を分ける機能が実装されるらしい。これまでも名前空間を自由にbindすることは出来たけど、これがプロセス毎に独立して出来るようになるってことかな。Plan9ちっくで良いなぁ。

λ. アスペクト指向

「AspectJ 入門 : 初めての人へ」を読んだ。[ruby-list:32521]を読んで、アスペクト指向の具体的な実装を知りたくなったので。

λ. Le Webring francophone de gimp

というのがあるのを知った。

λ. hyperset

一昨日書いた最初の実装だと、Ω= {Ω}, A = {0..9}, ℘(X)をXの冪集合として、℘({℘³(Ω), ℘⁴(φ), {{A}}} ∪ A) を計算するのに一分以上かかっていたので、プロファイラの結果を見ながら色々とチューニング。約4秒まで縮まった。まだ不満はあるけど、とりあえずこんなもんか。

λ. 『新・土曜ワイド殺人事件—京都藁人形殺人事件』, とり みき, ゆうき まさみ

を読んだ。

λ. 『ラブやん 4』, 田丸 浩史

を読んだ。

λ. 『げんしけん 5』, 木尾 士目

を読んだ。

λ. 紅葉@SFC (3)

λ. SPASSで知識の論理を使って論理パズルを解く?

最近、論理パズルを解くのに使える様相論理のツールはないかと探していたのだけど、SPASSは結構使えそうな感じなので、SPASSで知識の論理を使って論理パズルを解いてみようと思った。

題材は、以前に「トランプの和と積のパズル」と様相論理で形式化したトランプの和と積のパズルに挑戦しようと思ったのだけど、いきなり挑戦するにはちょっと複雑すぎるので、もう少し簡単な問題にする。 何にしようか少し迷ったが、情報科学における論理 (情報数学セミナー)(小野 寛晰) の p.187 「論理パズルと知識の論理」で紹介されている、赤いぼうし (美しい数学 (5))(野崎 昭弘/安野 光雅) の話を使うことにした。この問題を非常に簡単に説明すると以下のようになる。

AさんとBさんがいて、少なくとも一人は赤い帽子を被っていて、赤い帽子を被っていない人は白い帽子を被っている。 ただし、二人とも他人の帽子の色は分かるが、自分の被っている帽子の色は分からない。 そして、Aさんが「自分の帽子の色が分からない」と発言した。 このとき、Bさんの被っている帽子の色は何か?　そして、Bさんは自分の被っている帽子の色が分かるか?

ちょっと考えると、Bさんの被っている帽子の色が赤で、そしてBさんもそのことを知ることが出来ることがわかる。これをSPASSで表現すると以下のようになる。 ここでコマンドラインオプションの -EMLTheory=7 は全ての様相がS5様相であること、すなわち到達可能性関係が同値関係であることを指定している。

% SPASS -EMLTheory=7 -DocProof RedHat.dfg
begin_problem(RedHat).

list_of_descriptions.
  name({* Red Hat *}).
  author({* Masahiro Sakai *}).
  status(unsatisfiable).
  description({* 「赤いぼうし」の問題 *}).
end_of_list.

list_of_symbols.
  predicates[ (a,0) % Aさんの帽子が赤
            , (b,0) % Bさんの帽子が赤
            , (Ka,0), (Ra,2) % Aさんが知っているという様相
            , (Kb,0), (Rb,2) % Bさんが知っているという様相
            , (E,0),  (Re,2) % 二人とも知っているという様相
            , (C,0),  (Rc,2) % 共通知識であるという様相
            ].
  translpairs[ (Ka,Ra), (Kb,Rb), (E,Re), (C,Rc) ].
end_of_list.

list_of_special_formulae(axioms, eml).
  % [E]P <-> [Ka]P∧[Kb]P
  formula( forall([x,y], equiv(Re(x,y), or(Ra(x,y), Rb(x,y)))) ).
  % [C]P <-> [E][C]P
  formula( forall([x,y], equiv(Rc(x,y),
                               exists([z], and(Re(x,z), Rc(z,y))))) ).

  % どちらかの帽子は赤である
  prop_formula( box(C, or(a, b)) ).  
  % AさんはBさんの帽子の色を知っている
  prop_formula( box(C, or(box(Ka, b), box(Ka, not(b)))) ).
  % BさんはAさんの帽子の色を知っている
  prop_formula( box(C, or(box(Kb, a), box(Kb, not(a)))) ).

  % Aさんは自分の帽子の色が分からない
  prop_formula( box(C, not(box(Ka, a))) ).
  prop_formula( box(C, not(box(Ka, not(a)))) ).
end_of_list.

list_of_special_formulae(conjectures, eml).
  % Bさんは「自分の帽子の色は赤である」ことを知っている
  prop_formula( box(Kb,b) ).
end_of_list.

end_problem.

これをSPASSに証明させると証明に成功し、この推論が正しいことが分かる。 ただし、box(Kb,not(b)) を証明させようとすると止まらなくなるようなので、推論が正しいことを確認することは出来ても、問題を解くのには使えないかも。

【2007-12-10追記】 上記の定義には問題があることに気がついた(止まらない原因に関係があるかは不明)。 [C]P は F(X) = [E](P×X) の単なる不動点ではなく最大不動点である必要があるようだ。 これは一階述語論理に翻訳すると [C] の到達可能性関係 Rc が [E] の到達可能性関係 Re の推移閉包(transitive closure)になっていることに対応するのだが、これが表現できていない。 色々考えたが、どうも推移閉包は一階述語論理では表現できないようだ。

【2007-12-16追記】 上記では公理には各前提条件に共通知識の様相をつけていたけど、これは不要だった。 何故ならば、共通知識の様相付きの論理式から導出できることは全部、様相の付いてない論理式からも「必然化(necessitation)」を使って導出できるため。 これは Mechanizing common knowledge logic using COQ (c.f. 20071217#p01)を読んで知ったのだけど、何故こんな簡単な事を自分気付けなかったのだろう……orz　あと、共通知識の様相を使わなくした場合でも停まらないのは変わらなかったので、共通知識の様相の形式化は停まらないのには関係なかった。

λ. “Conceptual Mathematics: A First Introduction to Categories” 第二版

そういえば、Conceptual Mathematics: A First Introduction to Categories の第二版が出るらしい。発売予定は来春 2009/2/28 。

• ハードカバー版
• ペーパーバック版

第一版ではハードカバー版は374ページ、ペーパーバック版は376ページだったのが、第二版では両方とも408ページになってる。内容も追加されてるのかな。

λ. PrimoPDFでPowerPointファイルをPDF化する際に余白を消す方法

Powerpointのスライドを人に渡すときや、Slideshareで公開する際にPDFに変換したいことはよくある。Powerpoint 2007 以降なら Microsoft の出しているプラグインを使えばいいし、Acrobatを持っていればそれを使えばいいと思う。 それらがない場合にはPrimoPDFなどを使ってPDF化することになるのだけど、PrimoPDFで普通にPDF化したら余計な余白がついてしまって困っていた。その消し方がわかったのでメモ。

まず、Powerpointのデフォルトのスライドのサイズは幅25.4cm, 高さ19.05cmになっているはず。 これはページ設定のダイアログで確認できる。

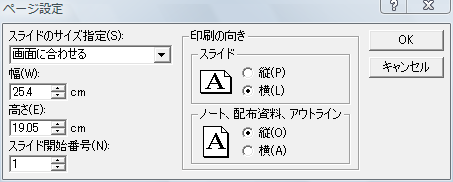
なので、用紙をこれにあわせて設定すれば良いだけ。 印刷時に「印刷」ダイアログのプリンタの「プロパティ」から、「PrimoPDF のドキュメントのプロパティ」というダイアログを開いて、「詳細設定(V)…」を選択すると、「PrimoPDF 詳細オプション」というダイアログが開かれる。

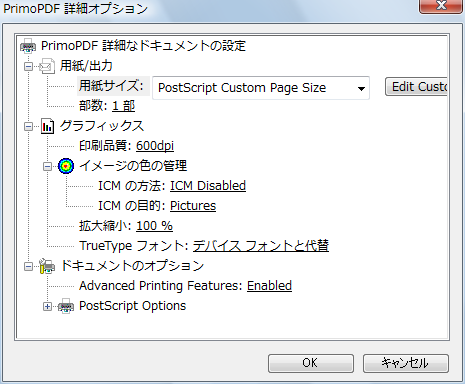
ここで、「PrimoPDF 詳細なドキュメントの設定 > 用紙/出力 > 用紙サイズ」で「Postscript Custom Page Size」を選ぶ。 「Postscript Custom Page Size Definition」というダイアログが開かれるので、「Unit」をMillimeterにして、「Custom Page Size Dimensions」で、さっきのスライドのサイズの縦横を入れ替えた Width: 190.50 、Height: 254.00 に設定する。 なぜ入れ替えているかというと、Powerpoint は横長の用紙であっても印刷内容を90度回転して印刷しようとするため。

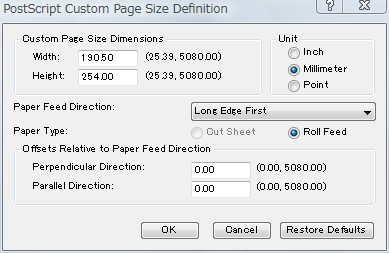
で、戻って印刷すると、今度は「PrimoPDF by Nitro PDF Software」という、PDFの生成オプションを設定するダイアログが出てくる。 どれを選んでも余計な余白のないPDFが生成される。

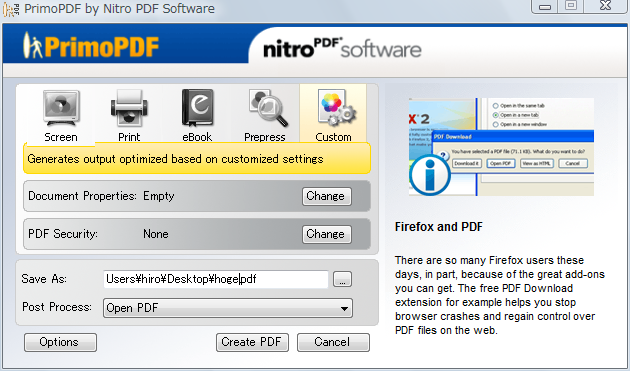
ただし、ここで「Print」「eBook」「Prepress」を選択した場合には90度回転されたPDFが生成されてしまう。これを避けるには「Screen」にするか、または「Custom」を選び「Auto-rotate Pages」を選択する。 もしくは、一度回転した状態のPDFを生成しておいて、RotPDF等の別ツールで回転させて直す。

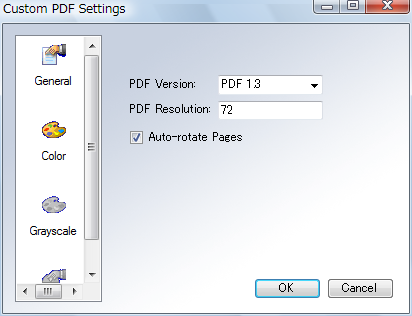
……とスクリーンショットまで用意して書いてみたものの、絶対にもっと簡単な方法がありそうだよなぁ。 一応、こないだの「自然言語をラムダ式で解釈する体系PTQのHaskell実装」のスライドはこの方法でPDF化してみたのだけど。