日々の流転

λ. 『風の大陸　 最終章　祈り』

読了。 最終巻だけ読んでなかったんだけど、ようやく読んだ。 最後はアッサリだったけど、ハッピーエンドでなにより。

λ. PLDIr #3

PLDIの論文を読む PLDIr の第三回に参加。 今回はPLDI99の論文が対象で、私は以下の3本の論文を紹介した。 今回は準備不足だったなぁ。

• Whole Program Paths
• What is a Recursive Module?
• Efficient Incremental Run-Time Specialization for Free

自分の発表資料(PDF, PPT):

前回は15:00開始で21時くらいまでやっていたけど、今回は18:30くらいで終了。

その後、筑波大の川島 英之さんにお会いし、DataLogがオーバーレイ・ネットワークの記述やネットワークの検証の分野で見直されているという話*1や Data Intensive Computing / Data Centric Computing 、徳永隆治先生の話など、色々面白い話教えてもらった。

λ. Thinkpadのプレゼンテーション・ディレクターの設定が消えて困った

ThinkVantage の SystemUpdate でアップデートを色々していたら、いつの間にかプレゼンテーション・ディレクター(Fn+F7で起動するやつでディスプレイを切り替えるやつ)のメニューの項目がすべて消えてしまって、困った。

結局、c:\Program Files\Lenovo\NPDIRECT\JP\NPDIRECT.INI の拡張子をnpdに変更したファイルを用意し、「オプション」「スキームのインポート」でこのファイルを読みこまさせることによって、デフォルトのメニュー項目は復元できたっぽい。自分で設定してたやつは消えたままだけど。

λ. iPhone で使うGoogle Reader のクライアントを RSS Flash g free から rss に乗り換えた

RSS Flash g free が起動しなくなったので、こないだ無料だったrssに乗り替えた。 UIはrssの方がiPhoneの標準的な感じだなぁ。 未読に戻す昨日が無いのは少し不満だけど、概ね満足。 これまで Feeds ⇒ RSS Flash g free ⇒ rss と乗り替えてきたが、Google Reader のクライアントひとつで、これだけ選択肢のあるiPhoneは……

λ. 『プログラミングHaskell』 Graham Hutton (著), 山本 和彦 (訳)

翻訳のレビューに参加させて頂いていた、『プログラミングHaskell』を献本していただきました。 また、それに加えて10月に出版された『プログラミングのための確率統計』も献本していただいてしまいました。 この場を借りて御礼申し上げます。

これまで日本語で出版されていたHaskellの入門書の『ふつうのHaskellプログラミング―ふつうのプログラマのための関数型言語入門』や『入門Haskell―はじめて学ぶ関数型言語』といった本は、ちょっとしたツールやゲームやWikiといった日常的な題材を通じてHaskellの使い方を学ぶという感じだったが、この本はそういうアプローチの本ではなく、「Haskellプログラマはどのように考え、どのようなモノの捉え方をするのか」というのを、もっとダイレクトに教えてくれる本。 そういう意味では、最後の章がアプリケーションの実装等ではなく、『プログラムの論証』という章であるのは象徴的だと思う。

というわけで、手っ取り早くHaskellで何が出来るのかを知るには向いていないけど、Haskellの考え方を知るにはオススメ。また、長年授業で使われてきた講義資料が元になっているだけあって内容の構成も洗練されているし、翻訳の質も高いと思う。

• Ohmsha 『プログラミングHaskell』
• 訳者によるサポートページ
• プログラミングHaskell - あどけない話(2009-11-04)

λ. 『プログラミングのための確率統計』 平岡 和幸 (著), 堀 玄 (著)

『プログラミングHaskell』と併せて、10月に出版された『プログラミングのための確率統計』も献本して頂いてしまいました。 この本は『プログラミングのための線形代数』と同じ著者らの本で、『プログラミングのための線形代数』で目から鱗の連続だった身としては、読むのが非常に楽しみです。 ありがとうございました。

• 『プログラミングのための確率統計』非公式サポートページ

λ. “A semantics for imprecise exceptions” by Simon Peyton Jones, Alastair Reid, Tony Hoare, Simon Marlow and Fergus Henderson

• <URL:http://doi.acm.org/10.1145/301618.301637>
• 著者版

こないだのPLDIr#3で稲葉さんが簡単に紹介していた論文。

CPUによってはアウトオブオーダー実行によって、単純に逐次実行する場合とは発生するエラーが異なってしまう場合がある。同様にHaskellのような純粋関数型言語でも、プログラム変換によって発生するエラーが異なってしまう場合がある。これがタイトルの imprecise exception の意味。

アウトオブオーダー実行やプログラム変換のような最適化によって意味が変わってしまうのは問題だけど、だからといってこれらを諦めるたり制限することは最適化のための大きな機会を逃すことになる。そこで、そのような変換によって意味が変わらないような意味論をかんがえるというのがこの論文。

まず、ゼロ除算エラーのような、起こる原因と場所がわかっているような例外(同期的例外)は、Haskellでは(手続き型言語における例外とは異なり)浮動少数点数のNaNのように式の値として伝播される(概念的には)。 そこで、式の表示的意味を通常の値もしくは起こり得る(同期的)例外の集合とする。その上で、例外の観察はIOアクションの中でしか出来なくして、この例外の集合から非決定的に一個取り出すという解釈をする。IOアクションの実行の意味論は神託を用いることを許しているので、これは問題ない。

このようにすることで、意味論上の問題もほぼ解決できて、かつ実装上も起こり得る例外を実際に全部集めたりする必要がなく効率的に実装できる。

起こり得る例外の集合を考える際の領域は Smyth Powerdomain の構成を利用しているのだけど、普通の関数型言語の意味論だとPowerdomainはなかなか見かけないので、「おーっ」と思った。

それから、Conclusion が As usual, implementation is ahead of theory: で始まっていて 笑った。

関連

• Christopher Krauß さんという方による紹介スライド

λ. “Asynchronous Exceptions in Haskell” Simon Marlow, Simon Peyton Jones, Andrew Moran and John Reppy

• <URL:http://doi.acm.org/10.1145/378795.378858>
• 著者版

割り込み・メモリ不足・タイムアウトといった、プログラムそのものの意味とは直接関係せずに発生するような例外を非同期的例外という。 非同期的例外は A semantics for imprecise exceptions でも一応扱われていたが、この論文では、非同期的例外の一種として、あるスレッドから別スレッドへの例外の送出を、より積極的にスレッド間のシグナリング機構ととして活用できるようにする。

あるスレッドから別のスレッドを殺したり例外を送出したりというのは、予期しないところで実行が中断することによって不変条件が成り立たなくなってしまう可能性などがあり、手続き型言語では色々悩ましい問題があった。一方、関数型言語では、プログラムの大部分を占める純粋な計算に関してはこのような問題はなく、そのため別スレッドへの例外の送出を積極的に活用しやすい素地がある。

もちろん、IOアクションの実行、特にスレッドの同期に関わる部分では手続き型言語の場合と同じ問題がある。この論文では例外の受け取りを遅延する状態でアクションを実行する block :: IO a -> IO a, 例外を受け取れる状態でアクションを実行する unblock :: IO a -> IO a という関数を利用してそのあたりの問題を扱う。

アクション二つを並行に実行して、どちらか先に結果を返した方を全体の結果にするようなeitherアクション、それからeitherを利用して書かれたtimeoutの実装がかっこよかった。今GHCに合わせると以下のような感じ。

import Prelude hiding (either, catch)
import Control.Exception
import Control.Concurrent

data EitherRet a b = A a | B b | X SomeException

either :: IO a -> IO b -> IO (Either a b)
either a b = do
  m <- newEmptyMVar
  block $ do
    a_id <- forkIO $ catch (do r <- unblock a
                               putMVar m (A r))
                           (\e -> putMVar m (X e))
    b_id <- forkIO $ catch (do r <- unblock b
                               putMVar m (B r))
                           (\e -> putMVar m (X e))
    let loop = catch (takeMVar m)
                     (\e -> do
                        throwTo a_id (e :: SomeException)
                        throwTo b_id e
                        loop)
    r <- loop
    killThread a_id
    killThread b_id
    case r of
      A r -> return (Left r)
      B r -> return (Right r)
      X e -> throwIO e

timeout :: Int -> IO a -> IO (Maybe a)
timeout t a = do
  r <- either (threadDelay t) a
  case r of
    Left _ -> return Nothing
    Right a -> return (Just a)

λ. Project Euler レベル3

Project Euler で100問を解き、レベル3になった。正六面体から正八面体に進化した。 記念すべき100問目は Problem 108 。

λ. “The Physical World as a Virtual Reality” by Brian Whitworth

うーん。確かに「情報」というのが物理法則のなかで本質的な役割を果たしているという話は色々あって、そういう話の延長として世界が一種のヴァーチャルリアリティとして実現されていると考えるのは自然とは思う。ただ、この人の言っている話って、あまりに安直なコジツケなんだよな。 質量の高い物体の周りで空間が歪曲するのは処理落ちのせいだとか、不確定性原理によってある2つの物理量の組み合わせを同時に観測できないのは、2つの属性が同じメモリを使っていたとしたら説明できるとかさ……。 あと、「観察者(observer)」に関する話とかも変だと思う。

そういえば、Programming the Universe が積読になってしまってるのを思い出した。

λ. コナミスポーツクラブ

コナミスポーツクラブに先日会員登録して、今日もまた行ってきた*1。 今日はまず30分くらいでの器具の使い方のインストラクションを受けてきた。それが終わったあとは何をしようかと思ったのだけど、とりあえずサイクリングマシンで体力測定して、あと500mだけ泳いできた。 しかし、体力測定で体力年齢48歳とかでたのはまいったね。確かに体力のある方ではないけど、最近は一応定期的に運動しているのになぁ。この測定の基準データの母集団、どんだけ健康なんだよ。

λ. HIMA #2 「Typeclassopedia」

今回は The Typeclassopedia の話。

関連

• ログ
• The Monad.Reader Issue 13 (The Typeclassopedia 原文)
• The Typeclassopedia 日本語訳
• 自分で作る Num の instance - あどけない話 (2009-11-16)

λ. 第五十八回圏論勉強会

今日は圏論勉強会。

今回は P. Selinger, “A survey of graphical languages for monoidal categories”の 5 Traced categories の残り。 Example 5.21 の symmetrical traced category だけど compact closed でない例が面白かった。

λ. 自然言語をラムダ式で解釈する体系PTQのHaskell実装

Haskellナイトの Lightning Talk “Haskell Gong”で発表してきた。

スライド(PDF, PPT)

今回の発表はタメになる話というよりは雑学的な話で、これを聞いて「へぇ」と思って、ちょっとでもモノの見方が変わってくれれば嬉しい。

なんでこういう発表をしたかという理由は2つ:

1. 関数型言語は非常に論理的で秩序だっているのに対して、自然言語は非論理的で無秩序と思われがちだけど、実は自然言語にもきれいな構造があるということを知って欲しい。
2. 関数型は現実世界から乖離した考え方だと思われがちだけど、そんなことはなくて、現実世界にも色々なところに関数型的なものがあるということを知って欲しい。その一例としての「自然言語」。

なお、元ネタである Richard Montague の“The Proper Treatment of Quantification in ordinary English”は1973の論文で、当時Lispは既にあったけど、MLやHaskellのような型付きの関数言語はまだ存在しなかった。ただ、型付きの関数型言語が普及した現在の方がむしろ彼のやったことは理解しやすいはず。

関連リンク

• PTQのHaskell実装
• HackageDB: PTQ
• デモサイト
• ソースコード(github)

余談

余談ながら、このスライドが Slideshare の Hot on Twitter に一瞬だけ入っていて、ちょっと嬉しかった。

λ. Haskellナイト

(後で書く)

座談会は想像以上に面白かった。 また、cut-sea さんがHaskellを始めるきっかけのひとつが、LL Weekend での僕の「その場でどう書く」だったというのは非常に嬉しかった。

他の方の感想など

• Haskell night にいってきた - クラなんとか or くらなんとか or cla なんとかの日記
• Haskell Night 行ってきました - Hatena::Diary::pi8027
• Haskell Night 2009 - ヤドカリデンキ商会（第一倉庫）
• Parsec 3活用事例: Keepalived構文チェッカ - maoeのブログ

λ. True Intensionality in Higher Order Logic

Logic and Engineering of Natural Language Semantics 6 (LENLS VI) での Reinhard Muskens 氏によるチュートリアル。 昨日の Haskell Night で紹介したMontagueのPTQのように自然言語の意味を形式的に考えることは形式的意味論と呼ばれて研究されていて、PTQはその最初期のものになる。 昨日PTQについて紹介して、今日このチュートリアルってのは偶然なのだけど、形式意味論の研究で僕がちゃんと知っているのはPTQくらいなので、最近はどんな感じなのかと思い、聞きに行ってきた。

タイトルの「Intensionality」というのは「内包」のことで、「内包」の取り扱いは形式的意味論を考える際のポイントの一つ。例えば、「明けの明星」と「宵の明星」はどちらも金星を指す、すなわち同じ外延を持つ言葉であるにも関わらず、「古代人は宵の明星を宵の明星だと信じていた」と「古代人は宵の明星を明けの明星と信じていた」は明らかに異なる意味を持っているので、「明けの明星」と「宵の明星」は異なる内包を持っていると言える。

チュートリアルのメモ

チュートリアルの最初の話は、PTQで〈s,t〉という型だった命題をprimitiveな型pとして扱う話。PTQだと「Mary believes that the cat is out if the dog is in.」と「Mary believes that the cat is in. 」から、「Mary believes that the dog is out.」を導出出来てしまうが、Maryは論理的に含意されることを全て推論可能とは限らない(imperfect reasoner)ので、これは一般には正しくない。そこで、命題の型としてpという型を導入して、必要に応じて〈s,t〉に変換する。それによって、前述のような誤った導出を出来なくする。

次の話はMoschovakisの「Fregeのsenseをalgorithms、Fregeのreferenceをvaluesと同一視する」というアイ ディアに基づいて、論理プログラムとして解釈する話。これまで、命題から可能世界の集合への関数を使って意味を形式化していたが、関数の代わりに、部分関数を表すニ項関係にする。 そして、意味公準(Meaning Postulates)を論理プログラム、命題をクエリーとして、Refutationをによって可能世界の集合を求める。自己言及的な命題ではRefutationが発散する。論理プログラムのRefutationの形で、実際の推論過程を取り込んでいるのが興味深い。

次は、命題をprimitiveとして扱うアプローチと似ているけど異なるアプローチの話。命題をprimitiveとして扱うのではなく、論理的に可能な世界を表す述語Ωを導入して、and/or/notなどの非論理定数はそれらの世界でのみ標準的な解釈をするようにする。

最後が、関係に基づいた高階の型理論の話。型として基本型とn≧0個のタプル型があって、関係に対してラムダ抽象とか適用とか出来て、解釈は内包と外延をうまく使い分けて定義されている。で、型〈〉で命題を、型〈〈〉〉で可能世界を扱ったりする。この論理は結構キモいけど面白かった。

α型の項の内包はD_αの要素とするのだけど、D_{〈α1, …, αn〉}の要素には外延というのがあって、これはD_α1×…×D_αnの部分集合になる。 命題の型〈〉の内包の領域はD_〈〉で、その外延の領域は一点集合のベキ集合になるので二点集合となり、これは{true, false}とみなせる。 可能世界の型〈〈〉〉の内包の領域はD_〈〈〉〉、外延の領域は命題の領域D_〈〉のベキ集合となる。

その他

@MoCo7さんに久しぶりにお会いし、また@kaleidotheaterさん、@zoeaiさん、@bon_jaさんといった方々に知りあうことが出来て良かった。 どうせなので、昨日の Haskell Night でのPTQの話についても紹介してみた。ただ、これは時間他の制約からかなりいい加減な紹介になっているので、専門の研究者に見られるのは恥ずかしいものがあるけど (^^;

それから、Combinatory Categorial Grammar (CCG) という範疇文法の一種を教えてもらった。

λ. ダイビングのレッスン

(後で書く)

λ. 慶應義塾大学SFC ORF2009【Gardens for Ingenuity -断面の触感-】

ORFに初めて参加し、今頃になってSFCって実は凄かったんだと感じる。以下、個人的に印象に残っている話をいくつかメモ。

個人的に面白かった展示のひとつが、「SF-KEY: 鍵盤楽器奏者のための譜めくり支援システム」で、演奏がどれだけ進んだかを自動認識して自動的に譜めくりしてくれるシステムを目指していた。現時点では自動認識の部分はできていて、画面上で楽譜の表示を切り替えることはできてるが、将来的には紙の楽譜をめくるようにしたいそうだ。

それから、ARのために目のまえに走っているクルマとデータを対応付けるために、どうするかという話なんかも面白かった。 ナンバープレートを画像認識して、そこから同定良いかと思ったのだけど、それは難しいらしく、代わりにテールライトの点灯タイミングを元に同定する方法を考えた、という話。

我らが萩野服部研の展示は、「どこでもIRプラグ」「S3」 「Acti-on」 「RIO」。

• 「どこでもIrプラグ」はSheevaPlugみたいなものをコンセントに指しておいくことで、赤外線リモコンで操作可能な家電を、外出先からWeb操作可能にするという話。デモとして、ORF会場から研究室の照明を操作するというデモをしていたが、元々研究室の照明は赤外線で操作なんて出来ないので電子工作を頑張っていて、むしろそっちの方が凄かったかも。
• S3 (Simple Sound Streamer) は、リスナーの選択した色をもとにメタデータのマッチングを行って、プレイリストをつくると言うもの。
• Acti-on は AR っぽい話だった。
• RIOについては何も言うまい(笑)。なんでも、今の萩野服部研には「お絵かき部」があるとか……

熊坂研のコミュニティ分析系の話で「声優偏愛マップ」「我輩は童貞である。まだやったことはない。」「リア充のリアリティ」とかあって、題材が狙いすぎな感じだけど、結構面白い結果が出ていて面白かった。

他にも、最適な量子通信路の決定の話とかみたいな話とか、触手がウネウネ動いてるやつとか、相変わらず随分色々やっているな、という感じ。

他にも面白い展示が沢山あった。

λ. PrimoPDFでPowerPointファイルをPDF化する際に余白を消す方法

Powerpointのスライドを人に渡すときや、Slideshareで公開する際にPDFに変換したいことはよくある。Powerpoint 2007 以降なら Microsoft の出しているプラグインを使えばいいし、Acrobatを持っていればそれを使えばいいと思う。 それらがない場合にはPrimoPDFなどを使ってPDF化することになるのだけど、PrimoPDFで普通にPDF化したら余計な余白がついてしまって困っていた。その消し方がわかったのでメモ。

まず、Powerpointのデフォルトのスライドのサイズは幅25.4cm, 高さ19.05cmになっているはず。 これはページ設定のダイアログで確認できる。

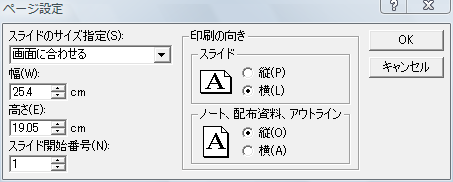
なので、用紙をこれにあわせて設定すれば良いだけ。 印刷時に「印刷」ダイアログのプリンタの「プロパティ」から、「PrimoPDF のドキュメントのプロパティ」というダイアログを開いて、「詳細設定(V)…」を選択すると、「PrimoPDF 詳細オプション」というダイアログが開かれる。

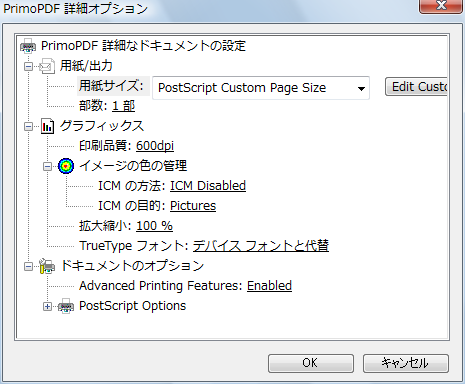
ここで、「PrimoPDF 詳細なドキュメントの設定 > 用紙/出力 > 用紙サイズ」で「Postscript Custom Page Size」を選ぶ。 「Postscript Custom Page Size Definition」というダイアログが開かれるので、「Unit」をMillimeterにして、「Custom Page Size Dimensions」で、さっきのスライドのサイズの縦横を入れ替えた Width: 190.50 、Height: 254.00 に設定する。 なぜ入れ替えているかというと、Powerpoint は横長の用紙であっても印刷内容を90度回転して印刷しようとするため。

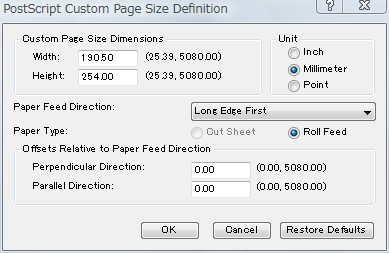
で、戻って印刷すると、今度は「PrimoPDF by Nitro PDF Software」という、PDFの生成オプションを設定するダイアログが出てくる。 どれを選んでも余計な余白のないPDFが生成される。

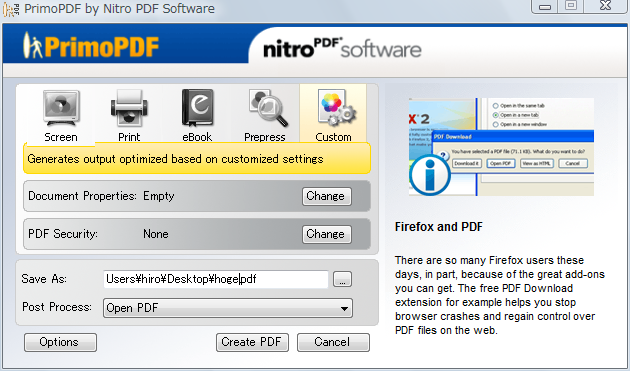
ただし、ここで「Print」「eBook」「Prepress」を選択した場合には90度回転されたPDFが生成されてしまう。これを避けるには「Screen」にするか、または「Custom」を選び「Auto-rotate Pages」を選択する。 もしくは、一度回転した状態のPDFを生成しておいて、RotPDF等の別ツールで回転させて直す。

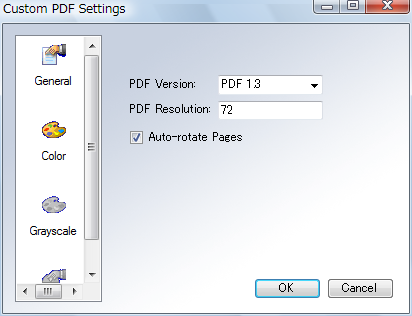
……とスクリーンショットまで用意して書いてみたものの、絶対にもっと簡単な方法がありそうだよなぁ。 一応、こないだの「自然言語をラムダ式で解釈する体系PTQのHaskell実装」のスライドはこの方法でPDF化してみたのだけど。

λ. 祖父の葬儀

(後で書く)

λ. 『数学』を数学的に考える

某所で紹介されていたので、読んでみた。扱っている内容は以前に読んだ「算術的階層の厳密性と形式的手法の限界について」とほぼ同じなのかな。

帰納法をΣ_n論理式に制限した IΣ_n というのが出てくるのだけど、これが有限公理化可能と書いてあって驚く。 そのことをTwitterに書いたら、ytbさんが「Hajek-Pudlakのp78に載ってます(定理2.52)。Σn論理式に関する真理述語を使うと、IΣ1の有限部分理論において、Σn論理式をそのゲーデル数と同一視でき、Σn帰納法の公理図式を一つの公理として表現できるとか。」とサクっと答えてくれて、「おお、なるほどー」と思った。 もっとも、これが気になった理由は、有限公理化出来ると定理証明器的に嬉しいのではと思ったためだったので、Σ_n論理式に関する真理述語を使うとなると全然嬉しくなさそうだけどね。

それと、照井先生は「文レベルの局所的な循環性ではなく、対象数学とメタ数学の大域的な循環性に目を向けるべき」と言っていて、そういえばこないだの数学基礎論サマースクール2009の Cut-elimination and Algebraic Completion でも「個別に論理を作ってカット除去とかを証明してというのではなくて、そもそも証明論の限界とは？」という話をしていたのを思い出す。 すごく大域的な視野というかビジョンを持って数学をしている感じがして、やはり凄いと思った。