2008-03-01 [長年日記]
λ. 大岩元先生・古川康一先生 合同最終講義・演奏会
今日は「Hasなんちゃら」もあったそうだけど、こっちに参加。 古川先生にはAbduction勉強会を初めとして、とてもお世話になっていたので、行こうと思っていたのだった。
最終講義は、「第5世代コンピュータからスキルサイエンスへ」というタイトルから、先日の渕一博記念コロキウム『論理と推論技術：四半世紀の展開』(c.f. ヒビルテ(2007-10-20))のときの「帰納・発想論理プログラミングとスキルサイエンス」と同様の話かと思っていたが、自伝的な内容であり、楽しく聞くことが出来た。
もっとも、メインはその後の演奏会だったわけだけど。
それから、色々な人に久しぶりに会えたのがうれしかった。特に、大学にはいって最初の学期(2001年春学期)にとった「論理プログラミング」の授業で一緒だった何人かの人に随分久しぶりに会えたのは楽しかった。
ビデオ
演奏会で演奏していた曲
今日演奏してた曲をナクソス・ミュージック・ライブラリ(NML)で探してみた。
- ハイドン (1732–1809)：ディヴェルティメント第一番 変ロ長調
- ファルカシュ (1905–2000)：17世紀のハンガリー古典舞曲集
- チャイコフスキー (1840–1893)：管弦四重奏曲第一番 ニ長調 作品11 より 2楽章：アンダンテ・カンタービレ
- ドヴォルジャーク (1841–1904)：弦楽四重奏曲「アメリカ」 作品96より 2楽章：レント
- ラフマニノフ (1873–1943)：ピアノとチェロのためのソナタ ト短調 作品19
- 鳥の歌
他の方の日記等
2008-03-02 [長年日記]
λ. AmazonモバイルでEdy!キャンペーン
「Amazonモバイルで、Edyを使って1,500円以上のお買い物をすると、抽選で170名様にステキな賞品が当たります」というキャンペーンをやっていたので、また注文してみた。ちょっと前に LIFE Books online (boox.jp) で注文したばかりなので、また注文するのはなにやら環境にやさしくなさそうで、少しばかり後ろめたいけど。
![[ライトアップされた日本庭園]](./images/20080305_0.jpg)
![[昨夜の雪が残る日本庭園]](./images/20080306_0.jpg)
2008-03-07 [長年日記]
2008-03-08 [長年日記]
λ. sized-list の append
PPL2008の懇親会でzyxwvさん、yoshihiro503さんと話していたときに出た話(の一つ)。
以下で定義される、サイズ情報を型に持つようなリスト型があったとする。
data Z
data S n
data List n a where
Nil :: List Z a
Cons :: a -> List n a -> List (S n) a
このリスト型に対して連結(append)を定義したいのだが、どうやって型を付けるかというのが自明ではない。
関数従属性を使う方法 (ダメな方法)
class Plus m n o | m n -> o instance Plus Z n n instance Plus m n o => Plus (S m) n (S o) append :: Plus m n o => List m a -> List n a -> List o a append Nil ys = ys append (Cons x xs) ys = Cons x (append xs ys)
これは一見うまくいきそうだが、第一引数がNilの場合であっても、GHCは List n a と List o a が同じ型であることを認識してくれず、型エラーとなる。 これは関数従属性の落とし穴と同じ問題。
GADT の type refinement を利用する方法
data Plus m n o where
PlusZ :: Plus Z n n
PlusS :: Plus m n o -> Plus (S m) n (S o)
append :: Plus m n o -> List m a -> List n a -> List o a
append PlusZ Nil ys = ys
append (PlusS n) (Cons x xs) ys = Cons x (append n xs ys)
関数従属性の場合と違って、GADTのパターンマッチ時にはちゃんと type refinement が起こるので、型付け出来る。 が、適用する際にわざわざPlus型の値を与えなくてはならないのが面倒くさい。
専用の型クラスを使う方法
class Append a b c where
append :: a -> b -> c
instance Append (List Z a) (List n a) (List n a) where
append Nil ys = ys
instance Append (List n a) (List m a) (List o a) =>
Append (List (S n) a) (List m a) (List (S o) a) where
append (Cons x xs) ys = Cons x (append xs ys)
そりゃ出来るけどさぁ……何か色々負けた気分。
もう少し賢い定義も出来るけど、本質的にはあまり変わらないと思う。
型関数を使う方法
type family Plus m n type instance Plus Z n = n type instance Plus (S m) n = S (Plus m n) append :: List m a -> List n a -> List (Plus m n) a append Nil ys = ys append (Cons x xs) ys = Cons x (append xs ys)
GHCの開発版に導入されている型関数(type function)を使う方法が一番スマートか。GHCの型関数の詳細については Towards open type functions for Haskell と GHC/Type families - HaskellWiki を参照。
2008-03-09 [長年日記]
λ. 第三十八回圏論勉強会
今日は圏論勉強会。
The Haskell Programmer's Guide to the IO Monad — Don't Panic を読む二回目で、今回は関手と自然変換の部分を読んだ。次回はモナド。
ちなみに、圏論勉強会の会場はびぎねっとさまに貸していただいています。いつもありがとうございます。
λ. ライフカードPresents 真冬のホラーゲームキャンペーン
先日ライフカードを作ったときにやっていた「真冬のホラーゲームキャンペーン」というキャンペーンのVISAギフトカード3,000円が届いていた。わーい。
2008-03-10 [長年日記]
λ. 地域振興券の効果
2月のRHG読書会のときに地域振興券の効果が話題になった。 あれは地域の印刷屋さんで印刷したので、その分は確実に地域を潤していたとか。
が、個人消費を押し上げる効果はあまりなかっただろうと思う。少なくとも私の周りでは通常の現金支出を地域振興券で代替するばかりで、それによって支出が増えたなんて例は全く無かったしね。 経済企画庁の地域振興券の消費喚起効果等についてによれば「振興券によって喚起された消費の純増分は、地域振興券使用額の32%程度」とのことだけど、本当にそんなに影響があったのだろうか。
あと、某氏が「それでも、貯蓄の増加は銀行の貸し出し増加につながる」といったことを言っていたが、当時貸し出しを制約していたのは、優良な貸し先が少ないことや、自己資本比率の問題であって、貸し出しの原資が不足していたからではない(そもそもゼロ金利政策のため低コストでいくらでも日銀から調達出来た)のだから、預金額の増加が効果を及ぼし得たとはとても思えないんだよな。
λ. A Module System for Agda by Ulf Norell
ふと見かけたので、読んでみた。 ちょっと前のスライドだけど、Agda2のモジュールシステムについて。
- モジュールは名前とスコープを構造化する。一方レコードはデータを構造化する。
- モジュールとレコードを区別し、モジュールそれ自体は型(や圏論的な意味)を持たない単純なモジュールシステムを採用。
- スコープチェックと型チェックの分離。
2008-03-11 [長年日記]
λ. 民主党的には低金利政策は悪なのか?
週末にTVを見ていたら、自民党が時期日銀総裁に推している現副総裁の武藤氏について、民主党の鳩山由紀夫幹事長が「低金利で国民に多くの損害を与えた責任」を反対の理由に挙げていて眩暈が。 そのときは聞き間違いかと思ったが、民主党の「日銀「武藤総裁」に不同意 役員会で党議決定」という記事にも「バブル経済、超低金利政策に対する反省がみられない」とかあるし……
不況時の金融緩和自体は当たり前だし、当時利上げなんかしていたら景気が更に悪化して国民に大きな損害を与えたことは疑いないと思うんだが、民主党は一体何を言ってるんだ!? 意味が分からない……
【2008-03-17 追記】 低金利と財政政策、金融政策 - lethevert is a programmer (2008-03-13) で言及されていた。 一応補足しておくと、財政政策に言及していないのは「金融政策は財政政策よりも有効」と考えているからではなく、財政政策に関わりなく、また金融政策に限界があるにしても、金利を低水準に抑えるのは当然の政策だからです。
【2008-03-18 追記】 この件に関して民主党の言っていることのデタラメさについては、現在の民主党に政権担当能力はないね - svnseeds' ghoti! (2008-03-11) が良くまとまっている。
【2008-03-25 追記】 泥酔論説委員の日経の読み方(2008-03-19)で知ったのだけど、民主党「次の内閣」は2003/01/29時点の「当面のマクロ金融政策について」では、量的緩和などの政策を継続・強化することを主張していた。
λ. 圏論の講義をYouTubeで
YouTube - TheCatsters's Playlists に圏論の講義のビデオがたくさん。自然変換、モナド、随伴、Hopf代数、etc., 講義をしているのは高次元圏論の研究者の Eugenia Cheng 女史という方らしい。素晴らしい! wrong, rogue and log : モナドの講義をYoutubeで より。
2008-03-12 [長年日記]
λ. 『笑わない数学者』のビリヤードの問題をAlloyで
先日、笑わない数学者―MATHEMATICAL GOODBYE (講談社文庫)(森 博嗣) の劇中に登場した5つのビリヤードの玉のパズルを Mathematical Goodbye. -笑わない数学者からの挑戦状- クイズ＆パズルの部屋「Quizzical Days.」 というところで見た知人に、解の一意性について聞かれた。
昔読んだときには、まじめに考えた気がするけど、また考えるのは面倒なので Alloy Analyzer に解かせてみることに。以下がAlloyで書いたモデル。
sig Ball {
num : one Int,
next : one Ball,
}
fact {
all b : Ball | int 1 <= int b.num && int b.num <= int 15
all b1 : Ball | all b2 : Ball {
b1.num=b2.num implies b1=b2
b2 in b1.^next
}
#Ball = 5
}
sig Cnt {
ball : one Ball,
val : one Int,
next : lone Cnt
}
fact {
all c1 : Cnt {
(no c2 : Cnt | c1=c2.next) implies c1.val = c1.ball.num
all c2 : c1.next {
c2.ball = c1.ball.next
c2.val = int c1.val + int c2.ball.num
}
no c2 : c1.^next | c1.ball = c2.ball
}
}
pred show() { }
run show for 5 Ball, 0 Cnt, 6 int
pred goal() {
all n : Int |
(int 1 <= int n && int n <= int 21) implies
some c : Cnt | c.val=n
}
run goal for 5 Ball, 25 Cnt, 6 int
残念ながら解けなかったけどね。
なお、一意性の証明はぐぐればどこかで見つかるでしょう(投げやり
2009-03-01 追記
これを書いたときは Alloy の sum の構文について知らなかったので地道に足し算をしていたが、sumを使うようにしたら、ちゃんと解けた。あと、Alloyでパックマン - らくがきえんじんで「sig ... in ...」という構文について知ったので、それも使ってみている。
abstract sig Ball {
num : one Int,
next : one Ball
}
one sig B1, B2, B3, B4, B5 extends Ball {}
fact {
all x : Ball | 1 <= x.num && x.num <= 15
#(Ball.num) = 5
next = B1->B2 + B2->B3 + B3->B4 + B4->B5 + B5->B1
}
pred connected[S : set Ball] {
all x, y : S | y in x.*((next + ~next) & (S -> S))
}
sig s01, s02, s03, s04, s05, s06, s07, s08, s09, s10,
s11, s12, s13, s14, s15, s16, s17, s18, s19, s20,
s21 in Ball { }
fact {
B1.num = 1
connected[s01] && sum s01.num = 01
connected[s02] && sum s02.num = 02
connected[s03] && sum s03.num = 03
connected[s04] && sum s04.num = 04
connected[s05] && sum s05.num = 05
connected[s06] && sum s06.num = 06
connected[s07] && sum s07.num = 07
connected[s08] && sum s08.num = 08
connected[s09] && sum s09.num = 09
connected[s10] && sum s10.num = 10
connected[s11] && sum s11.num = 11
connected[s12] && sum s12.num = 12
connected[s13] && sum s13.num = 13
connected[s14] && sum s14.num = 14
connected[s15] && sum s15.num = 15
connected[s16] && sum s16.num = 16
connected[s17] && sum s17.num = 17
connected[s18] && sum s18.num = 18
connected[s19] && sum s19.num = 19
connected[s20] && sum s20.num = 20
connected[s21] && sum s21.num = 21
}
pred show { }
run show for 5 Ball, 6 int
実行結果
Executing "Run show for 6 int, 5 Ball" Solver=minisat(jni) Bitwidth=6 MaxSeq=4 Symmetry=20 33024 vars. 430 primary vars. 114895 clauses. 365ms. Instance found. Predicate is consistent. 10741ms.
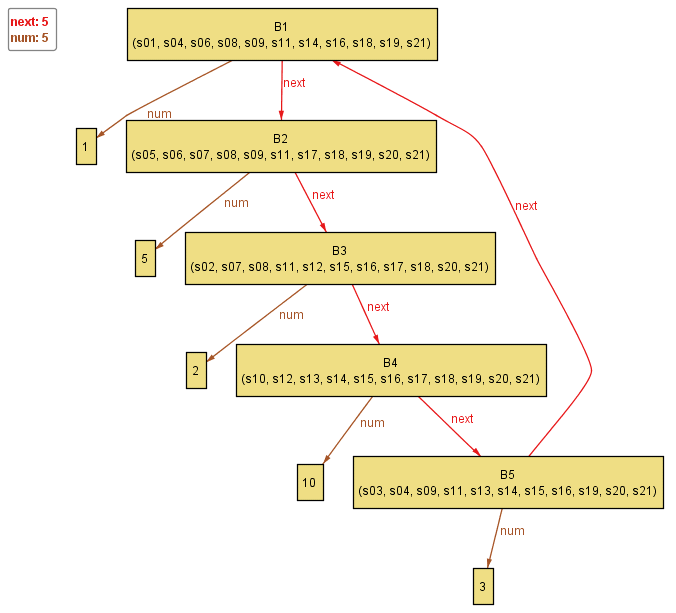
ここで、次の解を計算させると逆周りになった解が出てきて、さらにその次の解を計算させると今度は解無しになる。ので、解の一意性も確認できた。
2008-03-13 [長年日記]
λ. “Continuations in Natural Language” by Chris Barker
自然言語における継続 - sumiiの日記 で住井さんに教えてもらって、ずっと積読になっていたんだけど、今度の Continuation Fest 2008 の予習のために読んだ。「自然言語」で「継続」ときて連想したのは「そういえばPTQでの名詞句と量化子の扱いはCPS変換に似てるな」だったんだけど、ちょうどそれが最初の例として取り上げられていた。他の例としてはfocus, 等位接続(coordination), misplaced modifiers が取り上げられていた。これは面白い。
2008-03-14 [長年日記]
λ. 新銀行東京
破綻処理することになると、ひょっとしてペイオフ解禁後の初ケースになるのかな。ちょっと興味津々。金利が高かったこともあり、預金保険制度で保護される1千万を超えて預けている人が9千人以上、総額300億円以上あるとかだけど……
【追記】 金利が高かったことについては、西日本新聞の「高金利預金２１５０億円 新銀行東京、負担要因に」という記事によれば、「１・７％と１・５％の高めに設定した金利で集めた定期預金の残高が１月時点で２１５０億円に上り、残高総額約４０００億円の半数を超えている」とのこと。
2008-03-15 [長年日記]
λ. 某カードの限度額引き下げ
某クレジットカードの限度額が無駄に大きかったので、デスクに電話して引き下げてもらった。引き上げの申請はWeb上で出来るのに、引き下げは電話する必要があるのがなんとも。
2008-03-16 [長年日記]
λ. 花粉症?
ここ一週間くらい目が痒い＆鼻水出まくりで、認めたくないけどこれは花粉症なんだろうなぁ。一昨年はちょっと痒いくらいで、去年は特に症状はなかったのだが、今年はついにという感じ。 何か悔しいので昨年までと違う何かが原因なんじゃないかと考えてみたら、今年は中国製(?)のヒマワリの種を貪っていることがあった。ひょっとして……まあ濡れ衣だろうけど。
![[ヒマワリの種のパッケージ]](./images/20080316_0.jpg)
![[ヒマワリの種]](./images/20080316_1.jpg)
2008-03-17 [長年日記]
λ. 第68回情報処理学会・プログラミング研究会
ytbさんが「再帰的定義を可能にする述語論理の証明支援系上の実装」という発表をするようなので、お会いしに行きたいなぁ、と思っていたが、それどころじゃないのだった。
2008-03-18 [長年日記]
λ. “Category Theoretical Semantics for Pregroup Grammars” by Anne Preller
pregroup grammar における導出の圏論的な意味論。Lambek Pregroup - ヒビルテ (2005-01-07) で書いたのは大体あっていて、自由コンパクト2-圏(free compact 2-category)というものを考える。
2-圏がコンパクトであるのは全ての1-セルが左右の随伴を持つとき。 で、圏Cから生成される自由コンパクト2-圏T(C)は、0-セルをただ一つ持つ2-圏で、Cの対象を1-セルとし、Cの射を2-セルとして自由生成されるコンパクト2-圏。 T(C)の1-セルはCの対象の列でpregroupの要素に対応し、2-セルは一種のラベルつきグラフで pregroup grammar における導出に対応している。
例えば、以下の図は s : C→B, r : B→A, t : A→D を圏Cの射としたときの、ABlBClCllBlAlBC → DBCl という導出の例。
![[導出の例の図]](./images/20080318_0.png)
コンパクト閉圏との関係
ところで、コンパクトと聞くと、檜山さんがよく紹介しているコンパクト閉圏(compact closed category)を連想するわけで、確かに定義も似ているように思う。ので、ちょっと考えてみた。
まず、0-セルがただ一つであるような2-圏は1-セルの結合をモノイド演算と思うと厳密モノイダル圏(strictly monoidal category)になっている。この厳密モノイダル圏に更に1-セルの左右の随伴を加えたものがここで考えているコンパクト2-圏。一方、(厳密な)コンパクト閉圏は厳密モノイダル圏に1-セルの左随伴と対称性を加えたもの。 つまり、檜山さんは「コンパクト閉圏 - Chimaira.org」で「なんで『左』？」と書いていたが、この枠組みで考えると1-セルの左随伴にちゃんとなっている。
さらに、厳密モノイダル圏としてのコンパクト2-圏に対称性σを追加すると、(厳密な)コンパクト閉圏になるのは定義からして明らか。逆に対称性があればAの左随伴Alと右随伴Arは同じになるので、(厳密な)コンパクト閉圏は実際には左随伴だけでなく右随伴を持っていることになり、対称性を持つコンパクト2-圏になっている。
そう考えると、(1-セルをただ一つ持つ)コンパクト2-圏は(厳密な)コンパクト閉圏の非対称版と考えることが出来そうだ。 檜山さんは「コンパクト閉圏 - Chimaira.org」で「左随伴は、必ずしも対称でないモノイド圏でも定義できる（が、非対称ケースで意味があるのだろうか？ 僕はよく分からない）」と書いていたが、対称でないモノイダル圏における左随伴にも意味があったようだ。
2008-03-19 [長年日記]
λ. iKnow!のSkypeキャンペーンでSkype無料クーポンげっと
iKnow! + Skypeキャンペーン 結果発表。 iKnow賞とDictation賞で5位入賞でSkype無料クーポン2時間分をゲット。 数回しかやっていない私が入賞だなんて、参加人数が少なかったんだろうなぁ。
![[お菓子の小山]](./images/20080319_0.jpg)
2008-03-20 [長年日記]
λ. Firefox で PDF を開こうとすると Could not launch Acrobat と言われる
なんか知らないが、Firefox で PDF を開こうとすると “Could not launch Acrobat” というエラーが発生するようになってしまった。
解決法を探してしばらく駈けずり回ったが、結局 MozillaZine Forumの書き込み を参考に、Acrobat Reader の 編集 → 環境設定 → インターネット → Webブラウザオプション の三つのチェックボックス「PDFをブラウザに表示」「Web表示用に最適化を許可」「バックグラウンドでのダウンロードを許可」を一回外して、もう一回チェックしなおしたら直った。
わけがわからん。 ……コンピュータなんか嫌いだっ。
λ. 萩野服部研納会
毎年年度末にやっている納会。 今年は中華ではなく北海道炉端と有機無農薬野菜の浜蔵というところで。 久しぶりに集まると、やっぱり楽しいものだな。
2008-03-21 [長年日記]
λ. 飲み会
店員さんの裾が高めの浴衣と素足に萌え。
λ. 書き換え系について少し勉強 (「潜在帰納法と書き換え帰納法の比較」 by 小池広高 and 外山芳人)
私はどうも項書き換え系の話についてよく分かっていなくて、こないだも随分的外れなことを言ってしまった気がするので、ちょっと勉強してみようと思った。 何か短い入門的なテキストがあると良いのだけど、とりあえず手元にあった「潜在帰納法と書き換え帰納法の比較」(by 小池広高 and 外山芳人)というのを読んでみる。 以下は単なる感想で、内容の解説はない。
帰納的定理
まず、項書き換えシステムでは、帰納的定理とは任意の基底頂上で成立する等式のことを「帰納的定理」と呼ぶ。 さらっと片付けられているが、ここで少し悩んでしまった。
最初にちょっと悩んだのは、何で単に「定理」ではなくわざわざ「帰納的定理」と呼ぶのか。 任意の基底項上で成立するということはつまり始モデル(initial model)で成り立つということだけど、始モデルで成り立つ等式であっても新たな要素(junk)が加わったモデルでは成り立たない可能性があるので、帰納的定理は普通の意味での定理になっているとは限らないからか。
それから、次に悩んだのは何故「帰納的」という言葉を使うか。 ググってみると、始モデルにおける定理だからという話と、証明に一般に項の構造に関する帰納法が必要となるからという説明があるようだ。 両者は表裏の関係といっても良いので、これも納得。
潜在帰納法と書き換え帰納法
「潜在帰納法」は名前からして隠蔽代数(hidden algebra)における帰納法みたいなものだと勝手に思いこんでいたが、そうではなかった。
潜在帰納法(inductionless induction)も書き換え帰納法(rewriting induction)も、いずれも証明したい等式を追加した書き換え系が、(始モデルにおいて)元の書き換え系と同等であることを示すことによって、証明したい等式が元の書き換え系における帰納的定理であることを示す方法。
とりあえず、定義を確認して証明を一通り追いかける。 項書き換え系に詳しくないので結果については「へー」と思うだけなのだが、項書き換え系ではではこういう議論の仕方をするのね。面白い。
退行
弱正規化性、強正規化性、合流性は馴染み深い概念だけど、退行(Retrogresse)についてはまだイメージがわかないなぁ。
2008-03-22 [長年日記]
![[ビューティフルコードのチラシなど]](./images/20080322_0.jpg)
![[わらじ]](./images/20080322_1.jpg)
λ. チベット問題は格差問題でもあるのか?
伊藤洋一の Round Up World Now! の昨日の放送分を聞いていたら、チベット問題について、民族問題・宗教問題だけでなく、格差問題としての側面に着目した解説をしていた。 他ではあまりこういった解説を聞いたことがなかったので、興味深かった。
2008-03-23 [長年日記]
λ. The Disciplined Disciple Compiler (more than lambdas)
Disciple is an explicitly lazy dialect of Haskell which supports destructive update, computational effects, type directed field projections and some other useful things.
- Uses a typed core language which includes effect, closure, region and mutability information.
- This extended type information is used to allow code-transformation style optimizations in the presence of side effects and mutable objects.
- Compiles via standard C99, so is highly portable.
- Compiles cleanly on linux-x86 and darwin-x86 (tested on Mac OS X 10.5.2)
- Is in a usable alpha state.
[Haskell-cafe] ANN: The Disciplined Disciple Compiler - alpha 1 より。 面白そう。
(後で書く)
2008-03-24 [長年日記]
λ. バトン
随分前にかもねさんのmixi日記から回ってきてたバトン。 当時は音楽はほとんど聴いていなかったので答えられなかったけど、iPod nanoを入手 してから少しは聴くようになったので、今なら答えられるかな。
- ■コンピュータに入ってる音楽の容量は？
- 今のラップトップのiTunes Music Library だと 2416曲 / 6.4日 / 11GB 。 他のマシンにあるのも含めるともうちょっとある。
- ■今聞いている音楽は？
- 広有射怪鳥事 〜 Till When? - ピアノ独奏版 -
- ■最後に買ったＣＤは？
- こないだ色々懐かしい曲が聴きたくなって買った安室奈美恵の181920(TETSUYA KOMURO/KAZUMI SUZUKI/TK/NATSUMI WATANABE/TAKAHIRO MAEDA/MARC/DAVE RODGERS/YASUHIKO HOSHINO/COZY KUBO/安室奈美恵)。 その前は、このあいだの冬コミで買った「東方文鳥録 〜Return Reanimateness〜」 かな。
- ■よく聞く、もしくは思い入れのある５曲
-
- Shakira 「Ojos Así」
- Shakiraはいいよね。この曲は特にエキゾチックな雰囲気が好き。
- Bei Xu 「A Happy New Year」
- iTunes Store のフリーダウンロードで入手した曲のなかで一番再生回数の多い曲。
- Тату 「Простые движения」
- PVが色々な意味で印象に残っている曲。(PVは<URL:ftp://ftp.tatu.ru/Taty-Prostie_dvizhenia.avi>からダウンロードできるけど、<URL:http://www.youtube.com/watch?v=v1htcyGYyzY>で見たほうが早い)
- Sound Holic 「Mont Saint Michæl Et Sa Baie (Vocal Mix)」
- 同人CDから一曲。
- 篠原涼子 「恋しさと せつなさと 心強さと」
- 初めて買ったCD。
- ■自分の好きな異性のタイプは？
- 自分をしっかり持ってる人・他人にやさしく出来る人。しぐさのかわいい人。
- ■今行きたい所は？
- 旅行とかの趣味はないので特になし。
さすがにもう回したりはしません。
λ. Kowalskiの講演をまた聞き逃す
今日は第69回人工知能基礎問題研究会(SIG-FPAI)の一部としてKowalski教授の講演(講演概要「Problems of Logic Programming」)があったのだけど、すっかり忘れていて聞きにいけなかった。 そういえば、2006年に来たときも2002年に来たときも聞き逃しているんだよな。……うーん、残念なことをした。
それから、その後に予定されていた「論理プログラミングの現在、過去、未来」という題でのKowalski先生を交えたパネル(パネリスト 慶応大 古川康一先生、東工大 佐藤泰介先生、京大 山本章博先生)というのも面白そうで、こちらも残念なことをした。
あろはさんなどはよく論理プログラムをDISってるけどw、論理プログラミングにも面白い話はまだまだ沢山あるように思う。
関連
2008-03-25 [長年日記]
λ. 春雷
![[地面に散らばったヒョウ]](./images/20080325_0.jpg)
天気予報でも雨にはなっていなかったので、油断して折りたたみ傘も持たずに出かけてしまったら、帰りの電車を降りたときに雷雨になっててびっくりした。
しかも、ヒョウまで降ってくるし……ひどい目にあった。
2008-03-29 [長年日記]
λ. 論理プログラミングに思う
Kowalskiの講演をまた聞き逃す - ヒビルテ (2008-03-24)で「あろはさんなどはよく論理プログラムをDISってるけどw、論理プログラミングにも面白い話はまだまだ沢山あるように思う」と半分冗談で書いたら、ホワット・ア・ワンダフル・ワールド Prolog の思い出 で反応が。
もちろん論理プログラミングや関数プログラミングという枠組みでも，まだまだ面白い研究はできると思います．
ちなみに、私の書いた「面白い話」というのは、例えば(もはや古典的かもしれないけど)帰納論理プログラミングを用いたデータマイニングや、発想推論を用いた仮説の生成や、確率論理プログラミングを用いた確率モデリングといったものの応用の話で、それぞれの応用分野でそれなりに面白い結果が出ています*1。
これらは「論理による問題の記述」と「論理的な推論による問題解決」という論理プログラミングのアプローチの、まさに本流をいくものでしょう。
しかし，もうそういう狭いパラダイムの区別や慣習自体が古いんじゃないかなぁと．まだ黎明期には，他の研究分野との区別のための意味があったとはいえ，「論理」プログラミングや「関数」プログラミングという，歴史に由来する名前自体が重荷や偏見の原因になりつつあると思います．そろそろ，そういう過去にとらわれず，分野に分かれた研究成果を統合し，より高いレベルの知的プログラミングのための枠組みが必要なのではないかと思います．
うーん。「古い」と言われると、反発したくなるぞ(笑
論理プログラミングのような枠組みの中で考えるのは、そういった後ろ向きな理由だけでなく、単にそれが問題解決のための優れたアプローチだからというのが大きいのではないかと思います。 先に挙げたような例でも、論理という限られた枠組みでの形式化だからこそ上手く行っているわけで、より一般的な枠組みで考えることでより優れた問題解決のアプローチを実現することが出来るかといえば、そうとは限らないでしょうし。
統合されたより一般的な枠組みの意義は否定しないけど、そういった枠組みに基づいた問題解決のアプローチが、論理プログラミングのアプローチよりも優れたものになるまでは、論理プログラミングという枠組みの中で考えることは決して古くなどない、と私は思います。
*1 あろはさんも知っているとは思いますが。
2008-03-31 [長年日記]
λ. 新しい腰リール用のリール
![[リールアクション]](./images/20080331_0.jpg)
このあいだ腰リールのリールが切れてしまったので、帰りに丸善によって、たまたまあった PLU・S・CRUMのリールアクション(PT8-9 JAN 4512772 071172)というのを買ってみた。800円。半透明で中が透けるのは面白いけど、元々使ってた1200円のやつに比べるとやっぱり安っぽい感じがしてしまう。
ψ とおる。 [古川康一さんの『帰納論理プログラミング』という本をもっていますが、さかいさんの先生だったんですか。びっくり。]
ψ さかい [そうだったのです。 そういえば、とおるさん、以前に http://weblo.torus.jp/archives/0..]