2002-03-12
λ. 清水さんの夢に登場。:-)
λ. 生命って、恐ろしいほど強靭な面を見せたり、その一方で非常にあっけなく死んでしまったりする。生命に限らずこういう事を感じることは多い。昔からどうしてかなと思っていたのだけど、最近「つまりは我々を取り囲む世界のスケールの連続性に対して、我々の認識/視点が不連続だという事実に起因するのだな」と思うようになった。
う〜ん。うまく言いたいことが表現できないな。
λ. GTK+ 2.0
いまさらながらインストール。1.2とは共存できるから問題ないっすよー。
今Ruby/GTKを2.0でコンパイルしようとしてるんだけど、細かい変更が多くて苦戦中。そういえば、Ruby/GTK側で1.2用と2.0用のの共存に配慮するのかどうか気になる。
λ. 成績表(?)
届いた。最悪の事態は免れたが、やはり満足のいく結果ではない。自分のヘタれ加減に腹が立つ。
2005-03-12
λ. 独裁者占い
20世紀の独裁者であなたを占います。
Good Wrappers For People Who Love Bad Know-Hows (2005-03-09) より。
で、結果。
さかいさんは イディ=アミン です!
- あなたを独裁者にたとえると、ウガンダの独裁者イディ=アミンです。ガタイのいいあなたは、国民の畏怖のシンボルとなります。肉料理は好きですか?しばらくすると「食人大統領」なんていうタイトルであなたの映画ができるかもしれません。っていうかできます。あなたは亡命先でひっそりと息を引き取るでしょう。
- さかいさんの開運一人称は、「あたち」です!
- そんなあなたの本日の運勢はこちらです!
アミン様かよ…… orz
でも、ボカサ様でなくてまだ良かったと喜ぶべきなのかしらん。
λ. スズバキってなんだかブルバキみたいだ
とふと思った。suzuvakiとBourbakiで綴りは違うけれど。
λ. 読むのに手頃なHaskellのコード
いきなりGHCのコードを読むのはどうかと思うけれど、標準ライブラリは結構勉強になると思います。
あと、個人的に勉強になったものですぐに思いつくのは、Lazy Depth-First Search and Linear Graph Algorithms in Haskell とか Typing Haskell in Haskell のコードとかかなぁ。
λ. 第2回東方最萌トーナメント
紅美鈴が優勝しちまったよ……びっくり。
2007-03-12
λ. 算術的階層の厳密性と形式的手法の限界について
を読んでいる途中。 算術的階層って難しいものだとばかり思っていたけど、定義は簡単だし、しかもこんなに役に立つものだったんだな。
2008-03-12
λ. 『笑わない数学者』のビリヤードの問題をAlloyで
先日、笑わない数学者―MATHEMATICAL GOODBYE (講談社文庫)(森 博嗣) の劇中に登場した5つのビリヤードの玉のパズルを Mathematical Goodbye. -笑わない数学者からの挑戦状- クイズ&パズルの部屋「Quizzical Days.」 というところで見た知人に、解の一意性について聞かれた。
昔読んだときには、まじめに考えた気がするけど、また考えるのは面倒なので Alloy Analyzer に解かせてみることに。以下がAlloyで書いたモデル。
sig Ball {
num : one Int,
next : one Ball,
}
fact {
all b : Ball | int 1 <= int b.num && int b.num <= int 15
all b1 : Ball | all b2 : Ball {
b1.num=b2.num implies b1=b2
b2 in b1.^next
}
#Ball = 5
}
sig Cnt {
ball : one Ball,
val : one Int,
next : lone Cnt
}
fact {
all c1 : Cnt {
(no c2 : Cnt | c1=c2.next) implies c1.val = c1.ball.num
all c2 : c1.next {
c2.ball = c1.ball.next
c2.val = int c1.val + int c2.ball.num
}
no c2 : c1.^next | c1.ball = c2.ball
}
}
pred show() { }
run show for 5 Ball, 0 Cnt, 6 int
pred goal() {
all n : Int |
(int 1 <= int n && int n <= int 21) implies
some c : Cnt | c.val=n
}
run goal for 5 Ball, 25 Cnt, 6 int
残念ながら解けなかったけどね。
なお、一意性の証明はぐぐればどこかで見つかるでしょう(投げやり
2009-03-01 追記
これを書いたときは Alloy の sum の構文について知らなかったので地道に足し算をしていたが、sumを使うようにしたら、ちゃんと解けた。あと、Alloyでパックマン - らくがきえんじんで「sig ... in ...」という構文について知ったので、それも使ってみている。
abstract sig Ball {
num : one Int,
next : one Ball
}
one sig B1, B2, B3, B4, B5 extends Ball {}
fact {
all x : Ball | 1 <= x.num && x.num <= 15
#(Ball.num) = 5
next = B1->B2 + B2->B3 + B3->B4 + B4->B5 + B5->B1
}
pred connected[S : set Ball] {
all x, y : S | y in x.*((next + ~next) & (S -> S))
}
sig s01, s02, s03, s04, s05, s06, s07, s08, s09, s10,
s11, s12, s13, s14, s15, s16, s17, s18, s19, s20,
s21 in Ball { }
fact {
B1.num = 1
connected[s01] && sum s01.num = 01
connected[s02] && sum s02.num = 02
connected[s03] && sum s03.num = 03
connected[s04] && sum s04.num = 04
connected[s05] && sum s05.num = 05
connected[s06] && sum s06.num = 06
connected[s07] && sum s07.num = 07
connected[s08] && sum s08.num = 08
connected[s09] && sum s09.num = 09
connected[s10] && sum s10.num = 10
connected[s11] && sum s11.num = 11
connected[s12] && sum s12.num = 12
connected[s13] && sum s13.num = 13
connected[s14] && sum s14.num = 14
connected[s15] && sum s15.num = 15
connected[s16] && sum s16.num = 16
connected[s17] && sum s17.num = 17
connected[s18] && sum s18.num = 18
connected[s19] && sum s19.num = 19
connected[s20] && sum s20.num = 20
connected[s21] && sum s21.num = 21
}
pred show { }
run show for 5 Ball, 6 int
実行結果
Executing "Run show for 6 int, 5 Ball" Solver=minisat(jni) Bitwidth=6 MaxSeq=4 Symmetry=20 33024 vars. 430 primary vars. 114895 clauses. 365ms. Instance found. Predicate is consistent. 10741ms.
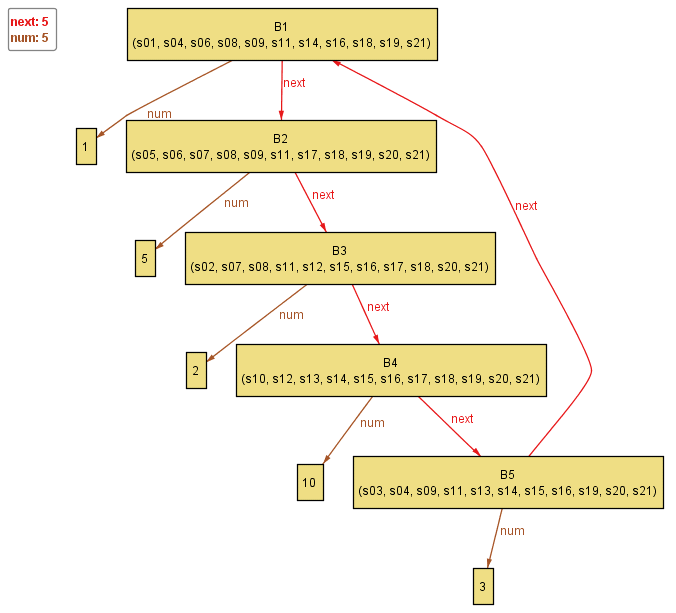
ここで、次の解を計算させると逆周りになった解が出てきて、さらにその次の解を計算させると今度は解無しになる。ので、解の一意性も確認できた。
