日々の流転

λ. 朝鮮語

期末試験。最悪の出来ですな。こりゃ単位を落としたに違いない。

落第者には3月頃までにメールが来るそうで……ドキドキ。

λ. 人工知能論

『脳のなかの幽霊』を読んだことのある人が僕の他に一人もいないというのは意外だった。あんな面白い本を読まないなんて、なんて奴等だ!! (ところで、森山さんによると「脳のなかの幽霊」は版元品切れらしい)

チェロの演奏を聴いていて、「人工知能/人工生命にとってのモノリスはやはり人間なのかな……」とか連想した。弦楽器の音色は、いつも思いがけないものを想起する。

それから、試験は持ち込み可。コンピュータも持ち込み可。

λ. マクロ経済Ⅰ

こんなの常識だと思ってたが、アブソープション・アプローチなんて名前があるのね……

λ. 変化の理論

とりあえず『現代の古典解析』は読書キューに入れておく。

λ. 講演「間違いだらけの擬似乱数選び」

これは聴きにいく鹿。

講演日時： 2月6日（水） 13:00-14:30
会場: o11
講演タイトル：　「間違いだらけの擬似乱数選び」
講演者：　松本　眞 （まつもと・まこと）
          京都大学 総合人間学部 基礎科学科・助教授
講演主旨と講師の紹介：

　コンピュータによる疑似乱数の発生法は、本質的に不確定性を含んだ現象のシミュレーションや暗号乱数を使ったコンピュータ通信のためには不可欠の基礎である。特に、物理や金融現象などのモンテカルロシミュレーションでは、極めて大規模に乱数が消費され、高品質の乱数を高速に発生させることができなければならない。しかし、これまでの方法では、物理のIsing Modelシミュレーションなどにおいて有意の誤差を生むことが報告され、その理論的欠陥が指摘されている。疑似乱数の研究とその利用 は混沌の歴史をたどってきたといえよう。

　松本助教授は、第24番目のメルセンヌ素数 ２^{19937}-1を周期とするMersenneTwister (MT)という疑似乱数発生アルゴリズム創り出した。MTは、これまでの疑似乱数発生法にあった様々の欠点を一掃し、メモリ効率、周期の長さ、乱数性、速度のすべての面 で画期的なアルゴリズムとして全世界から注目されている。MTの優れた乱数性は緻密な数論に基づいて証明されており、その実装は現代のコンピュータアーキテクチャを有効に反映したものとして実現されている。さらにMTを利用して並列乱数発生スキーム Dynamic Creator を開発し、超並列環境で高品質の疑似乱数を効率のよく発生させることも可能にした。 MTのアルゴリズムは様々の言語で実装されインターネットを通して配布され、物理、金融をはじめ世界中の極めて幅広い分野のユーザーに急速に広がっていき、高い評価を得ている。その一つとして、フェルミ研究所では、大きな周期性をもつ疑似乱数発生法としては現在最高のものであろうと評価されている。MTは、数論的概念とコンピュータアーキテクチャが美しく融合した疑似乱数発生法の尤物であり、世界標準の疑似乱数発生アルゴリズムとして位置付 けられるものである。

λ. MSN Messenger contact list to FOAF conversion

こないだ萩野研の誰かが「MSNメッセンジャのコンタクトリストあたりからFOAFを生成するのが良いのでは?」といっていたのを思い出し、簡単なスクリプト(msnmsgr2foaf.rb)を書いてみた。 サインインしている状態で実行すると標準出力にFOAFを出力する。まだ、作りこんではいないけど、雛形を作るくらいには使えるだろう。

が、その後ググってみたら [rdfweb-dev] MSN contact list to FOAF conversion というメールを見つけ、例によって同じ目的のツールがすでにあったと知る。

• MSN-to-FOAF
• msn2foaf

λ. SFU 3.5 で ruby をコンパイルしてる人の数 → (5)

というわけでコンパイルしてみる。

λ. Re: 街で見かけた数学用語

so1さんは とてもとても手が出せない遠い存在 といいますが、toposの概念自体はそんなに難しくないですよ。toposの定義はさておき、部分集合の概念を圏論の言葉で一般化したのがsubobjectですし、集合Xの部分集合Sに対応する特性関数 φ_S: X→{true,false} で、Sを部分集合からsubobjectに一般化するために、集合{true,false}を一般化したのがsubobject classifier (truth-value object) Ω です。
論理との関係にしたって、任意の集合が(部分集合を命題、集合演算子を論理演算子 として)古典命題論理のモデルになっているのと同様に、toposのobjectは直観主義命題論理のモデルになっている、というのが最初の話だったと思います。

もちろん、私の知識なんて微々たる物なので、 この先に奥深い話がきっと沢山あるんでしょうけどね。

ところで、Topos Theory in a Nutshellなんかにも書かれてますが、William Lawvere and Steve Schanuel, Conceptual Mathematics: A First Introduction to Categories, Cambridge U. Press, Cambridge, 1997. のtoposの入門はとても分かりやすかったです。それから、同じページで知ったのですが、Michael Barr と Charles Wells の Toposes, Triples and Theories ってオンラインで公開されているんですね。

λ. 第十三回圏論勉強会

今日は圏論勉強会。今回は田町の男女共同参画センターという場所だった。

写真

昼飯

昼飯の時に駅の反対側に行って何か見たことのある風景だなと思ったら、慶應の三田キャンパスがあるのが田町だった。気づかなかった……

Session 24 の Exercise 3 (p.268)

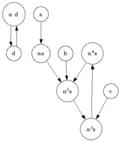
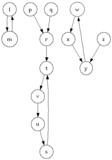
力学系(dynamic system) X^↻α と Y^↻β の表現(presentation)から力学系 X^↻α×Y^↻β の表現を求める方法を考える問題で苦戦してしまった。X^↻α の表現における生成元の集合をG_X、関係(等式の集合)をR_Xとすると、以下のようにすれば一応表現は得られると思うが、これだと生成元の定義が嫌な感じ。

生成元の集合

{ (x,y) | x∈X, y∈Y, x∈G_X∨y∈G_Y }

等式の集合

{ γ^min(m,i)(α^m-min(m,i)a,β^i-min(m,i)c) = γ^min(n,j)(α^n-min(n,j)b,β^n-min(n,j)d) | (α^ma = αⁿb)∈R_X, (a,b∈G_X), (βⁱc = β^jd)∈(R_Y∪R_Y^-1), (c,d∈G_Y)}
(ただしR_Y^-1はR_Yの等式の両辺を入れ替えたもの。)

図 (2006-02-01 追記)

X^↻α

Y^↻β

X^↻α×Y^↻β

λ. 初雪 (2)

一夜明けてこんな感じ。

λ. お菓子買いだめ

先月、20071220#p01でお菓子を買いだめしたけど、また買いだめしてみた。

λ. 不吉

以前に作って使っていた腰リールのリールが切れた。不吉だ……

λ. 初風邪

悪寒が酷い。これは風邪引いたな。12月にも酷い風邪を引いたばかりだったのでショックだ。 昨日、ちょっと喉の調子が悪かったのに、気にせず泳いでしまったのがまずかったか。 家に帰って暖かくしてたら38.5℃くらいまで体温が上昇。 一晩寝て直るといいなぁ。