2008-08-23 [長年日記]
λ. QMLから量子回路へのコンパイル
QMLで量子テレポーテーションの続きで、QMLのプログラムを実際にコンパイルして遊んでみる。出力先は色々選べるが、とりあえず型付きの量子回路へのコンパイルを試してみることに。qml.hsをghciで読み込んで、runTC "ファイル名" "識別子" とすれば、型付きの量子回路へと変換される。
Qnot
-- The quantum Not operation (Pauli X) Qnot (b,qb) |- ifo b then qfalse else qtrue :: qb;
まずはこのQnotをコンパイルしてみる。
Prelude QML> runTC "teleport.qml" "Qnot"
OK (TCirc {inT = {Q2}, outT = Q1 :<*> Q2, hpS = 0, gbS = 0, circ = Not})
inT が入力の「文脈」を表していて、outTは出力の「型」を表している。ただ、単なる Q2 ではなく Q1⊗Q2 になっているのは何でなんだろう。Q1⊗Q2 ≅ Q2 なので、構わないといえば構わないのだけど。
それから、hpS = 0 はヒープのサイズが 0 qubit で inT 以外の余計な領域を必要としないことを、gbS = 0 はゴミのサイズが 0 qubit で余計なゴミが出力されないことを表している。circ が回路本体で、ここでは単純なNotゲートになっている。
アダマール変換
-- The Hadamard operation
Had (b,qb) |- ifo b then hF * qfalse + (-hF) * qtrue
else hF * qfalse + hF * qtrue :: qb;
次にアダマール変換 Had の場合には「TCirc {inT = {Q2}, outT = Q1 :<*> Q2, hpS = 0, gbS = 0, circ = Seq (Rot (0.7071067811865475 :+ 0.0,0.7071067811865475 :+ 0.0) ((-0.7071067811865475) :+ -0.0,0.7071067811865475 :+ 0.0)) (Not)}」が得られる。
ここで、Rot (λ0, λ1) (κ0, κ1) は以下で定義されるユニタリー変換を表しているようだ。
- qfalse ↦ λ0 qfalse + λ1 qtrue
- qtrue ↦ κ0 qfalse + κ1 qtrue
これを行列で表すと ![\[\left( \begin{array}{rr} \lambda_0 & \kappa_0 \\ \lambda_1 & \kappa_1 \end{array} \right)\]](tex/5b5eb59120a323fedf0d9d74f7266cf1.png "\[\left( \begin{array}{rr} \lambda_0 & \kappa_0 \\ \lambda_1 & \kappa_1 \end{array} \right)\]")
になる。
Had の出力に現れる Rot の場合には、![\[\frac{1}{\sqrt{2}} \left( \begin{array}{rr} 1 & -1 \\ 1 & 1 \end{array} \right) = \left( \begin{array}{rr} 0.7 & -0.7 \\ 0.7 & 0.7 \end{array} \right)\]](tex/42d7b7eef0e40a5380949be3692064b3.png "\[\frac{1}{\sqrt{2}} \left( \begin{array}{rr} 1 & -1 \\ 1 & 1 \end{array} \right) = \left( \begin{array}{rr} 0.7 & -0.7 \\ 0.7 & 0.7 \end{array} \right)\]")
という行列を表している。
そして、Seq φ ψ は ψ ∘ φ という合成を表しているようだ。
Not も内部的には Rot (0,1) (1,0) で表現されているので、行列で表して計算してみると、通常のアダマール変換(Hadamard transform)になっているのが確認できる。
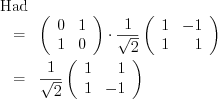
EPR
-- The constant EPR pair Epr |- hF * (qtrue,qtrue) + hF * (qfalse,qfalse) :: qb*qb;
これをコンパイルすると、TCirc {inT = {}, outT = (Q1 :<*> Q2) :<*> Q2, hpS = 2, gbS = 0, circ = Seq (Seq (Seq (Par (Hadamard) (Wire [0])) (Cond (Not) (Rot (1.0 :+ 0.0,0.0 :+ 0.0) (0.0 :+ 0.0,(-1.0) :+ -0.0)))) (Wire [1,0])) (Wire [1,0])}が得られる。
これまでの例と違っていて、通常の入力がないかわりに hpS = 2 で 2 qubit のヒープを必要とする回路になっている。ここでヒープと言っているのは単に qfalse で初期化された入力。
ここで、回路中の Par φ ψ は φ⊗ψ で回路を縦に並べたもの。 また、Cond φ ψ は (true, x) を (true, φ x) に、(false, x) を (false, ψ x) に写像する変換。
Hadamard を H、Not を X、Rot (1,0) (0,-1) を Z と書くことにすると、Eprは以下のように図示される。
![[EPRの図]](./images/20080823_0.png)
Bnmeas
Bnmeas (x,qb) (y,qb) |- let (xa,ya) = CNot (x,y)
in (Had (xa),ya) :: qb*qb;
Bnmeas は TCirc {inT = {Q2,Q2}, outT = (Q1 :<*> Q2) :<*> Q2, hpS = 0, gbS = 0, circ = Seq (Seq (Seq (Controlled-Not) (Wire [1,0])) (Wire [1,0])) (Par (Seq (Rot (0.7071067811865475 :+ 0.0,0.7071067811865475 :+ 0.0) ((-0.7071067811865475) :+ -0.0,0.7071067811865475 :+ 0.0)) (Not)) (Wire [0]))} になる。
上のアダマール変換のときの変換結果がそのまま入っているので長いけど、結局、以下の図で書ける。
![[Bnmeasの図]](./images/20080823_1.png)
U
-- The correction operations
Uol (x,qb) |- ifo x then qfalse else qtrue :: qb;
Ulo (x,qb) |- ifo x then -qtrue else qfalse :: qb;
Ull (x,qb) |- ifo x then -qfalse else qtrue :: qb;
-- The "unitary correction"
U (q,qb) (xy,qb*qb) |- let (x,y) = xy
in if x then (if y then Ull (q) else Ulo (q))
else (if y then Uol (q) else q) :: qb;
このUの場合には TCirc {inT = {Q2 :<*> Q2,Q2}, outT = Q1 :<*> Q2, hpS = 0, gbS = 2, circ = Seq (Seq (Wire [1,2,0]) (Cond (Seq (Cond (Seq (Rot ((-1.0) :+ -0.0,0.0 :+ 0.0) (0.0 :+ 0.0,1.0 :+ 0.0)) (Not)) (Seq (Rot (0.0 :+ 0.0,1.0 :+ 0.0) ((-1.0) :+ -0.0,0.0 :+ 0.0)) (Not))) (Wire [1,0])) (Seq (Controlled-Not) (Wire [1,0])))) (Wire [1,0,2])} にコンパイルされる。gbS = 2 なので本来の出力の他に 2 qubit のゴミが出ている。
Uの回路全体を考える前にまず部品から考えると、Uol, Ulo, Ull はそれぞれ以下のユニタリー変換にコンパイルされている。
![\[U_{01} = X = \left( \begin{array}{rr} 0 & 1 \\ 1 & 0 \end{array} \right)\]](tex/4c48e9697194294c7db020c47783a300.png "\[U_{01} = X = \left( \begin{array}{rr} 0 & 1 \\ 1 & 0 \end{array} \right)\]")
![\[U_{10} = Z = \left( \begin{array}{rr} 1 & 0 \\ 0 & -1 \end{array} \right)\]](tex/68a939d7e899c47a8d06f57276533f48.png "\[U_{10} = Z = \left( \begin{array}{rr} 1 & 0 \\ 0 & -1 \end{array} \right)\]")
![\[U_{11} = \left( \begin{array}{rr} 0 & 1 \\ -1 & 0 \end{array} \right)\]](tex/3499c80123b5dc41cc82921cc2f025b2.png "\[U_{11} = \left( \begin{array}{rr} 0 & 1 \\ -1 & 0 \end{array} \right)\]")
U全体はこれらを使った以下のような回路になる。
![[Uの回路図]](./images/20080823_2.png)
ここで、┤による終端が観測を表していて、観測結果がゴミになっている。観測が条件分岐よりも後になっているのは、The principle of deferred measurement を利用したものだろう。 しかし、この回路を見ると条件分岐がそのまま翻訳されているのがわかって、わかりやすいな。
Tele
-- The Teleport algorithm
Tele (a,qb) |- let (b,c) = Epr ()
in let f = Bnmeas (a,b)
in U (c,f) :: qb;
このTeleportをコンパイルすると TCirc {inT = {Q2}, outT = Q1 :<*> Q2, hpS = 2, gbS = 2, circ = ... } となる。流石に長くなるのでcircの式は省略。hsS = 2 なので 2 qubit のヒープを必要として、gbS = 2 なので本来の計算結果の他に 2 qubit がゴミとして出力されるような回路を表している。
回路本体は、既にコンパイルした Epr, Bnmeas, U を利用して以下の図のように表せる。
![[Teleの図]](./images/20080823_3.png)
まとめ
QMLで書かれた量子テレポーテーションのプログラムの量子ゲートへのコンパイルを適当に眺めてみた。 特に結論めいたものは何もないのだけど、量子計算というものがどんな感じのものなのか、ちょっと雰囲気は分かってきた気がする。
