日々の流転
プロフィール
カレンダー
| 前 | 2005年 11月 |
次 | ||||
| 日 | 月 | 火 | 水 | 木 | 金 | 土 |
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 | |||
日記内検索
タグ
本 | logic-programming | tDiary | 英語 | gimp | ruby | cygwin | scheme | gtk | quiz | 流行りもの | 時事 | 映画 | tom | TV | URL | w3m | ネタ | Web | 検索 | 論文 | 圏論 | haskell | javascript | machine-learning | メモ | 向井研 | CPL | 食 | ChannelTheory | linguistics | SemanticWeb | logic | 型理論 | 東方 | continuation | 後で | Topology via Logic | ocaml | modal-logic | theorem-proving | hiki | モデル検査 | 人狼 | programming-contest | agda | probability | quantum | 音楽 | coq | money | Alloy | lifehack | music | maude | プロセス代数 | thinkpad | game | security | linear-programming | optimization | Erlang | iPhone | mac最近のツッコミ
最近のトラックバック
日記は現代の病です。読み過ぎ書き過ぎはあなたの健康を害する恐れがあります。くれぐれもご注意下さい。
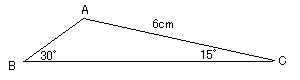

解けちゃった...
さっすが〜
僕のPCだと画像が真っ黒なんだけど、これあぶり出しとかじゃな(ry
うはwww、気づいてませんでした。IEだと真っ黒になりますね。<br>IEはアルファチャンネル付きのPNGはダメなのか……<br>透過色にしたのでこれでIEでも表示できるはず。
IEは8-bitのPNGならアルファをうまく表示できるけど、24-bitの場合はできないらしいです。
うは、IEの罠っすかwww<br>Firefox使ってたんだけど、なんかいかれてまともに動かなくなってしまったんよねぇ。<br><br>あ、ちなみに解けましたよ。補助線3本入れました。<br>初等幾何の問題なんて何年ぶりだろう。
ありゃ、補助線三本ですか。<br>僕の答えは補助線二本だったので、別解っぽいですね。<br>後で答えをうpしときます。
Aからの垂線とBAの延長で考えましたが。
BAの延長と、それへのCからの垂線で解ける気がするけど、その解き方はOKなのかなぁ
あぁ、BAの延長とCからの垂線の方がスマートですねぇ…<br>遥かに複雑な解き方をしてしまった。答えは一緒になりました。
僕が用意してた答えも「BAの延長とCからの垂線」でした。<br>たけをさんの「遥かに複雑な解き方」が気になります(^^;
http://www.osk.3web.ne.jp/~usitukai/images/hibirute.PNG<br>↑こんな感じでAD、AE、EFを引いて、ΔADCとΔEFCが相似であることからADの長さxの2乗x^2を求め、んで全体の面積が(1+√3)x^2になるので…って計算しました。あーしんど。
解けた.20分ぐらいかかってしまったよ...
ええと、正弦定理は反則ですか。
できた……。ぼくもたけをさんと同じやり方でした。<br>しかも三角形の辺の比を間違えて、30 分くらい悩んでしまいました。
>>たけをさん<br>それは確かに計算大変そうっすね。<br><br>>>とおる。さん<br>そういや正弦定理なんてもありましたね。<br>中学生向けの問題なので出題者の意図としては三角関数は無しだろうけど、個人的にはそういう方法も聞いてみたいです。
んーと、まず半角公式で sin 15°を求めて、正弦定理で各辺の長さがもとまるので、それを使ってヘロンの公式で面積が求まります。(たぶん。)<br><br>ちょうどさいきん、MEPHISTO を作っていて似たような計算をしたので、それが頭に残っていました(笑)。
なるほど。たしかにそれで出来そうですね。<br># ヘロンの公式とかすっかり忘れてて検索してしまいました(^^;