日々の流転

λ. 一階様相μ計算. 岡本圭史

<URL:http://www.nue.riec.tohoku.ac.jp/jssst2005/papers/05009.pdf>

一階様相μ計算(First-order Modal μ-calculus)の定義とその意味論は非常に素直。

μ計算についてはよく知らなかったのだけど、νX.φ(X) は μX.¬φ(¬X) と定義すればよいのかな。

不完全性を証明するのに、証明可能な論理式全体が帰納的枚挙可能(recursive enumerable)である一方、恒真な論理式全体が帰納的枚挙可能ではないということを証明している。常套手段みたいだけど、知らなかった。そのために、ω×ω循環タイル張り問題(recurrent tiling problem)を使っているのだけど、これは巧妙だなぁ。あと、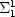-完全とはどういうことだろう?

【2006-03-31 追記】 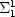はarithmetical hierarchyってやつか。解析集合(analytic set)の階層でも同様の記号が用いられるようだが、何か関係はある?

λ. 狂言師の和泉元彌がプロレスラーとしてデビュー

まじすか。

• <URL:http://www.asahi.com/culture/nikkan/NIK200510120015.html>

(追記) ハッスルってのはそういうところだったのね。納得。驚いて損した。

λ. るびま 0010 号

メモ。

λ. 飲み会＠ラパウザ

例のメンバで。

それから、ビリヤードをやって、その後 FF7 AC をみた。色々懐かしいな。