日々の流転

λ. PEGにマッチする文字列をAlloyで生成する

この間の正規表現にマッチする文字列をAlloyで生成すると同様のことを今度はPEG(解析表現文法)に対して行う。文字列の表現などは前回と同じ。

単純化するために、e* と e+ の e が非終端記号Nになるように文法があらかじめ変形されているものとする。

式に対する解釈は大体以下のような感じ。

• [[ ε ]](x,y) = (x==y)
• [[ c ]](x,y) = (x.tail==y && x.head==c)
• [[ N ]](x,y) = y in x.N
• [[ e1 e2 ]](x,y) = some z : String | [[ e1 ]](x,z) && [[ e2 ]](z,y)
• [[ e1 / e2 ]](x,y) = [[ e1 ]](x,y) || ((no z : x.*tail | [[ e1 ]](x,z)) && [[ e2 ]](x,y))
• [[ N* ]](x,y) = y in x.*N && (no z : y.^tail | z in y.N)
• [[ N+ ]](x,y) = y in x.^N && (no z : y.^tail | z in y.N)
• [[ e? ]](x,y) = [[ e / ε ]](x,y)
• [[ &e ]](x,y) = x==y && (some z : String | [[ e ]](x,z))
• [[ !e ]](x,y) = x==y && (no z : String | [[ e ]](x,z))

その上で解析規則の集合

N1 ← e1
…
Nn ← en

を

pred Rules(N1, …, Nn : String -> String)
  all x, y : String {
    y in x.N1 <=> [[ e1 ]](x,y)
    …
    y in x.Nn <=> [[ en ]](x,y)
  }  
}

として不動点を表す述語にする。 (これだと最小不動点であることは表せていないけど、Alloyでは最小性を直接記述できないので、とりあえずその辺りは気にしないことにする)

で、Niにマッチする文字列を適当に生成するには以下のようにする。

pred test() {
   some N1,…,Nn : String -> String {
      Rules[N1,…,Nn]
      some x : String | Nil in x.Ni
   }
}
run test for 10

具体例: A ← a A a / a

-- A <- a A a / a
pred Rules(A : String -> String) {
   all x, y : String {
      y in x.A <=> (p[A,x,y] || q[A,x,y])
   }
}
pred p(A : String -> String, x, y : String) {
   some z, w : String {
      x.head==C_a
      x.tail==z
      w in z.A
      w.head==C_a
      w.tail==y
   }
}
pred q(A : String -> String, x, y : String) {
   all z : String | !p[A,x,z]
   x.head==C_a
   x.tail==y
}

pred test() {
   some A : String -> String {
      Rules[A]
      some x : String {
         Nil in x.A
         all y : String | y in x.*tail
      }
   }
}
run test for 10

assert no_a5 {
   all A : String -> String |
      Rules[A] =>
          no x0 : String {
             let x1 = x0.tail |
             let x2 = x1.tail |
             let x3 = x2.tail |
             let x4 = x3.tail |
             let x5 = x4.tail {
                x0.head==C_a
                x1.head==C_a
                x2.head==C_a
                x3.head==C_a
                x4.head==C_a
                x5==Nil
                Nil in x0.A
             }
          }
}
check no_a5 for 10

assert uniq_A {
   all A1, A2 : String -> String {
      Rules[A1] && Rules[A2] => A1==A2
   }
}
check uniq_A for 10

実行例

Alloy Analyzer で「Run test for 10」を実行すると、「a」「aaa」「aaaaaaa」といった文字列を表すモデルが生成される。 例えば、「aaa」の場合にはこんな感じ。

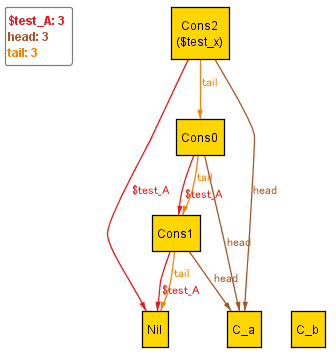
これを見ると二文字目と三文字目のaがAにマッチしているのに対して、一文字目のaはマッチしていないことがわかったりとかする。

一方、他のモデルの探索を繰り返しても「aaaaa」を表すようなモデルは生成されない。 そこで、「Check no_a5 for 10」を実行すると、「No counterexample found」となり、そのようなモデルが(多分)存在しないことが示せる。

関連

• PEG - d.y.d.