日々の流転

λ. パソコンと言えば……

「パソコンと言えば酒井」みたいな思い込みを勝手に流布しないで欲しいものだ。> 某方面

λ. 夕飯

お寿司。サビ抜きで頼んだのに、ワサビが入っているのがあった。がびーん。

λ. 情報射

情報射って何の訳なんだろう? Information Flow: The Logic of Distributed Systems という書名からして、Infomation Flow の訳?

λ. Kazumoto's Scientific BBS

.

λ. SFC-MODEのCommunity

CommunityをNNTPで読めたら良いのにと書いたけど、過去のメッセージの親子関係を取得するのが面倒だけど、あとは割と簡単そう。NNTPの勉強を兼ねて簡単なものを作ってみよう。

λ. 創作童話「博士(はくし)が100にんいるむら」

生存記録 (2005-05-05) 経由で、「博士が100人いるむら」のオチはマジなのか? より。

うはぁ……

λ. 秋葉原にて

天せいろ＠わらびや

餞＠芋蔵BAR

λ. イデアル完備化の落とし穴

完備化(completion)と呼ばれると、閉包(closure)なんかと同じで、冪等な操作であることを期待してしまう。Knuth-Bendix完備化手続きなんかも冪等だしね。しかし、イデアル完備化(ideal completion)は冪等ではない。

N = {0≦1≦…} のイデアル完備化は Idl(N) = {0≦1≦…≦∞} となる。 さらにイデアル完備化をすると Idl(Idl(N)) = {0≦1≦…≦∞´≦∞} となる。 ∞はIdl(N)ではコンパクトではないが、Idl(Idl(N))ではコンパクトになっているのに注意。

λ. PEGにマッチする文字列をAlloyで生成する

この間の正規表現にマッチする文字列をAlloyで生成すると同様のことを今度はPEG(解析表現文法)に対して行う。文字列の表現などは前回と同じ。

単純化するために、e* と e+ の e が非終端記号Nになるように文法があらかじめ変形されているものとする。

式に対する解釈は大体以下のような感じ。

• [[ ε ]](x,y) = (x==y)
• [[ c ]](x,y) = (x.tail==y && x.head==c)
• [[ N ]](x,y) = y in x.N
• [[ e1 e2 ]](x,y) = some z : String | [[ e1 ]](x,z) && [[ e2 ]](z,y)
• [[ e1 / e2 ]](x,y) = [[ e1 ]](x,y) || ((no z : x.*tail | [[ e1 ]](x,z)) && [[ e2 ]](x,y))
• [[ N* ]](x,y) = y in x.*N && (no z : y.^tail | z in y.N)
• [[ N+ ]](x,y) = y in x.^N && (no z : y.^tail | z in y.N)
• [[ e? ]](x,y) = [[ e / ε ]](x,y)
• [[ &e ]](x,y) = x==y && (some z : String | [[ e ]](x,z))
• [[ !e ]](x,y) = x==y && (no z : String | [[ e ]](x,z))

その上で解析規則の集合

N1 ← e1
…
Nn ← en

を

pred Rules(N1, …, Nn : String -> String)
  all x, y : String {
    y in x.N1 <=> [[ e1 ]](x,y)
    …
    y in x.Nn <=> [[ en ]](x,y)
  }  
}

として不動点を表す述語にする。 (これだと最小不動点であることは表せていないけど、Alloyでは最小性を直接記述できないので、とりあえずその辺りは気にしないことにする)

で、Niにマッチする文字列を適当に生成するには以下のようにする。

pred test() {
   some N1,…,Nn : String -> String {
      Rules[N1,…,Nn]
      some x : String | Nil in x.Ni
   }
}
run test for 10

具体例: A ← a A a / a

-- A <- a A a / a
pred Rules(A : String -> String) {
   all x, y : String {
      y in x.A <=> (p[A,x,y] || q[A,x,y])
   }
}
pred p(A : String -> String, x, y : String) {
   some z, w : String {
      x.head==C_a
      x.tail==z
      w in z.A
      w.head==C_a
      w.tail==y
   }
}
pred q(A : String -> String, x, y : String) {
   all z : String | !p[A,x,z]
   x.head==C_a
   x.tail==y
}

pred test() {
   some A : String -> String {
      Rules[A]
      some x : String {
         Nil in x.A
         all y : String | y in x.*tail
      }
   }
}
run test for 10

assert no_a5 {
   all A : String -> String |
      Rules[A] =>
          no x0 : String {
             let x1 = x0.tail |
             let x2 = x1.tail |
             let x3 = x2.tail |
             let x4 = x3.tail |
             let x5 = x4.tail {
                x0.head==C_a
                x1.head==C_a
                x2.head==C_a
                x3.head==C_a
                x4.head==C_a
                x5==Nil
                Nil in x0.A
             }
          }
}
check no_a5 for 10

assert uniq_A {
   all A1, A2 : String -> String {
      Rules[A1] && Rules[A2] => A1==A2
   }
}
check uniq_A for 10

実行例

Alloy Analyzer で「Run test for 10」を実行すると、「a」「aaa」「aaaaaaa」といった文字列を表すモデルが生成される。 例えば、「aaa」の場合にはこんな感じ。

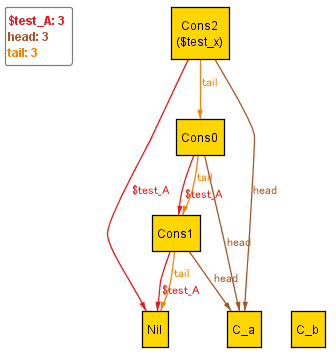
これを見ると二文字目と三文字目のaがAにマッチしているのに対して、一文字目のaはマッチしていないことがわかったりとかする。

一方、他のモデルの探索を繰り返しても「aaaaa」を表すようなモデルは生成されない。 そこで、「Check no_a5 for 10」を実行すると、「No counterexample found」となり、そのようなモデルが(多分)存在しないことが示せる。

関連

• PEG - d.y.d.

λ. Haskell→Isabelle

ranhaさんが書いていた　Haskabelle*1に少し興味を持つ。 HaskellプログラムをIsabelleに変換するものらしい。 マニュアルによると、例えば以下のようなHaskellプログラム

module Classes where

class Monoid a where
  nothing :: a
  plus :: a -> a -> a

instance Monoid Integer where
  nothing = 0
  plus = (+)

-- prevent name clash with Prelude.sum
summ :: (Monoid a) => [a] -> a
summ [] = nothing
summ (x:xs) = plus x (summ xs)

class (Monoid a) => Group a where
  inverse :: a -> a

instance Group Integer where
  inverse = negate

sub :: (Group a) => a -> a -> a
sub a b = plus a (inverse b)

が

theory Classes
imports Nats Prelude
begin
class Monoid = type +
  fixes nothing :: 'a
  fixes plus :: "'a => 'a => 'a"

instantiation int :: Monoid
begin
  definition nothing int :: "int"
  where
    "nothing int = 0"
  definition plus int :: "int => int => int"
  where
    "plus int = (op +)"
instance ..
end

fun summ :: "('a :: Monoid) list => ('a :: Monoid)"
where
"summ Nil = nothing"
| "summ (x # xs) = plus x (summ xs)"

class Group = Monoid +
  fixes inverse :: "'a => 'a"

instantiation int :: Group
begin
  definition inverse int :: "int => int"
  where
    "inverse int = uminus"
instance ..
end

fun sub :: "('a :: Group) => ('a :: Group) => ('a :: Group)"
where
  "sub a b = plus a (inverse b)"
end

というIsabelleの記述に変換されるとか。 Isabelleの構文をきちんと知らないので、良くは分からないけど。

ただ、Haskellのデータ型や関数をIsabelleの普通のデータ型や関数に変換しているため、変換結果はIsabelleに停止しない関数として拒絶されることがあるそうだ。 (その辺りはどうしているのかなぁ、と思ったら案の定)

調べてみると、HaskellからIsabelleへの変換の試みは他にもいくつかあるみたいだな。 Implementation of a Pragmatic Translation from Haskell into Isabelle/HOL はHaskabelleと同じくそのまま単純に変換している。 一方、Paolo Torrini, Christoph Lueth, Christian Maeder, Till Mossakowski. Translating Haskell to Isabelle は、Isabelle用の領域理論のライブラリであるIsabelle/HOLCFを使った領域理論的な記述へと変換しているので、扱いは面倒だけど、停止しない関数が拒絶されるといった問題は無い。

λ. Google Code Jam 2012 : Round 1B

調子が悪すぎて頭が全く働かず、C-small のみの Rank: 2943 Score: 6 (id: sakai) となってしまった orz 詳しくは後で書く。

• Participant Details: sakai ― Code Jam 2012 Statistic

Problem A. Safety in Numbers

.

Problem B. Tide Goes In, Tide Goes Out

.

Problem C. Equal Sums

.

λ. Google Code Jam 2012 : Round 1C

全問行けたと思ったら B Largeが間違ってて Rank: 79 Score: 73 (id: sakai)。 1Bが調子悪すぎだったので、なんとかパスできそうで嬉しい。 あと、C Smallの一番乗り達成！ 詳しくは後で書く。

• Participant Details: sakai ― Code Jam 2012 Statistic

Problem A. Diamond Inheritance

.

Problem B. Out of Gas

.

Problem C. Box Factory

.