原文: Thermodynamics and Garbage Collection. ACM Sigplan Notices 29, 4 (Apr 1994), 58–63.
Henry G. Baker Nimble Computer Corporation日本語訳: 酒井 政裕
私たちは統計力学の原理とそのストレージ管理の問題への適用について議論します。 また、私たちは 情報, 状態, 可逆, 保守的 といった用語の不正確な用法による問題について指摘します。
計算機科学者は抽象統計熱力学についての知識を持っているべきです。 まず、計算機システムは力学系(dynamical systems)であるという点で物理的な系と全く同様で、したがってその特徴付けの重要な最初のステップは時間に対して不変な性質やパラメータ(i.e., 運動定数)を見つけることです。 第二に、統計熱力学が系の巨視的な性質を大量の微視的な過程の統計的な振る舞いに還元することに成功したことがあります。 コンピュータシステムが小さな構成要素の集積になるにつれ、その巨視的な振る舞いも同様にその構成要素の集積された統計的振る舞いとして得られるかもしれません。 そこまでは言えなくとも、統計熱力学のアプローチのエレガントさは少なくとも新しいモデルへのインスピレーションを提供することができるでしょう[1]。 第三に、コンピュータシステムの構成要素は、物理的な統計熱力学の微視的な過程と同じサイズに近づきつつあり、したがってこれらへの知識はそれらの微視的な過程の能力によりよくマッチするコンピュータシステムを設計するのを助けることが出来ます。 例えば放熱を減らすとか。
自然熱力学は、マクスウェル以来、巨視的な性質と過程を多数の微視的な過程の統計的振る舞いに還元することから成っていました。 微視的な過程の詳細な振る舞いにはアクセス出来ないので、多数の微視的過程の集積された結果の振る舞いを考えざるを得ません。 適切な条件下では、平均化効果と中心極限定理が、微視的な詳細から独立した巨視的な性質と過程についてのほぼ確実な予測を可能にします。
コンピュータシステムはとても大きく複雑になったため、その微視的な過程の詳細な振る舞いを調査することは、もはや実り多いものではありません。 それには詳細な振る舞いに触れることが出来ないかも知れないからと、平均化効果が詳細な振る舞いを無関係にしてしまうかも知れないからという両方の理由があります。 現代的なオブジェクト指向システムのストレージ管理はそのような集積の適切な事例です。なぜなら、オブジェクトの数は膨大で、その微視的な詳細はアクセス出来ないかも知れないからです。 特に、並列性が非常に高くトランザクション(の分解能)が微視的な場合にはそうです。
統計熱力学は集積ないしは巨視的な振る舞いを微視的な振る舞いの統計から予測するので、まず最初にそれらの単語が何を意味するかを特徴づけなくてはなりません。 ここでは古典的(決定的)なモデルを仮定します。 つまり、系はwell‐definedな状態を持ち、状態と状態遷移関数からその系の将来の全ての状態を完全に予測可能だとします。 そのような完全な状態を私たちは微視的状態と呼びます。何故なら、系の巨視的な振る舞いだけでなく微視的な振る舞いをも完全に予測するのに必要な情報が全て含まれるからです。微視的状態の中身はしばしば粒子(particles)と呼ばれる個々の部分系の記述に分解されます。 微視的状態の各独立変数は自由度(degree of freedom)もしくは数学的に次元と呼ばれることがあります。典型的な巨視的なシステムの記述における、自由度もしくは次元の数はアボガドロ数(1023くらい)のオーダです。[2]
巨視的状態は微視的状態の、膨大な量の情報を無視するような数学的な射影です。 例えば、アボガドロ数個の次元を、温度や圧力といった一握りの巨視的な次元に射影します。多くの情報を捨ててしまう射影が、それにも関わらず集積の振る舞いを予測するのに役立つことは、熱力学の大きな成功です。 これは、すなわち準同型の性質が成り立っていて、ある微視的状態から射影された数が、将来の微視的状態から射影される数を予測するのに役立つということです。
射影である巨視的状態は多くの微視的状態の像であり、すなわち与えられた巨視的状態に当てはまる微視的状態は数多く存在します。 計算機言語のコンパイラは「生きている」レジスタの集合をプログラム中の各位置について計算しなくてはならない[Aho86]のですが、そこではこのような状況は一般的です。 プログラムの分岐には不確定性があるので、コンパイラが出来ることは(束における極限を計算することで)生きているレジスタの集合の近似を計算することだけです。 これらの束の要素が巨視的状態にあたり、それに対して動いているプログラムでのインストラクションの詳細な作用(の結果)は微視的状態にあたります。
ストレージ管理に伴う射影は明確です。 ストレージマネージャの設計者は(ストレージマネージャを呼び出す)アプリケーションプログラムの詳細な振る舞いにはアクセスしないし出来ませんが、少数のパラメータをもってアプリケーションの振る舞いを特徴づけなくてはなりません。 そして、ストレージマネージャの設計者は、アプリケーションを特徴付ける少数の巨視的なパラメータから、系の将来の集積された振る舞いを予測するでしょう。 幾つかの有益なパラメータは、オブジェクトの平均サイズ、オブジェクトのallocationレートの平均、オブジェクト解放レートの平均、オブジェクトの平均生存時間、オブジェクトのサイズや生存期間の分散、等などであるかも知れません。
分散システムでは、微視的状態や巨視的状態を整合的に定義することは難しいかもしれません。 なぜなら、分散している状態を計測する、整合的で大域的な時間の概念が必要となるからです。 私たちは現在のところそのような困難は無視することにします。
膨大な数の微視的状態を巨視的な視点で平均化するには微視的状態を数え上げ、重み付けしなくてはなりません。 状態を数え上げることは通常論争にはなりません。 なぜなら、コンピュータシステムは区別可能で数え上げ可能なwell‐definedな状態を持つからです。 より難しい問題は微視的状態をありそうな度合いによって重み付けすることです。 そして、系を分解するのに最も難しい作業は、独立な部分系を見つけ、系全体の性質を局所的な性質の和や積として計算できるようにすることです。 もし、それらの系が真に独立ならば数え上げや重み付けは乗法的で、われわれは数え上げや重み付けを快適に行うことが出来ます。 そして、この条件は統計的独立と呼ばれます。さらに、もしそれぞれの独立した部分系が十分単純(その全ての微視的状態が等確率)ならば、重み付けを系全体に容易に拡張することが出来ます。
状態の重み付けのプロセスが観測者の知識に依存することは避けられません。 古典的(すなわち決定的)な系で最初の微視的状態の完全な知識を持っている観測者は、各瞬間における系の微視的状態を正確に知ることが出来ます。 したがって各時間でただ一つの状態に対してのみ非ゼロの重みを割り当てるでしょう。 しかし、最初の微視的状態を知らないとしても、熱心で持続的な観察者は、最初のマクロ状態に当てはまる全ての微視的状態について網羅的にトレースする計算を行うことで、より正確な予測を行うことが出来ます。 もし、集積されたモデルの観察者が、最初の巨視的状態として与えられた情報全てを利用せず、その情報をトラッキングしないのであれば、その観察者は系の発展に伴い情報を失い続けるでしょう。 例えば、幾つかのアプリケーションは最初の入力の範囲が与えられたときに、「区間演算」を行い、答えの範囲を計算します。 不幸なことに、これらの範囲は計算過程での情報の損失によって、しばしば非常に悲観的なものになります。例えば、x が [1,3] の範囲にあるとして、x−x は [1,3] − [1,3] = [1−3,3−1] = [−2,2] の範囲となり、正確な範囲である [0,0] よりもかなり悪い結果になってしまいます。すなわち、区間演算は入力として与えられた全ての情報を保存するわけではありません。
計算機科学者は、現実それ自体と、現実についての観察者の知識とを正確に区別します。 しかし、2つの異なる気体を分離している区切りを除去することについての物理学者の説明の多くは、現実の気体の混合と、気体の混合状態についての観察者の無知とを区別していません。 しかし、誰でも、物理的に平衡が実現されるのは、区切りの除去よって観測者が無知になることによって引き起こされるのではないとを信じているはずです。 さらに、両方の観点からの計算が同じ数値的な答えを導くということよって、この混乱に拍車がかかっています。([Jaynes88]は「極大エントロピー」を無知として形式化することについて議論しています)
私たちは系の位相空間(phase space)を微視的状態の状態空間として定義します。 すなわち、各微視的状態は位相空間の一つの点です。 一つの巨視的状態は幾つもの異なる微視的状態の射影なので、各巨視的状態に関連付けられる位相空間の点は幾つも存在します。 ある巨視的状態に関連付けられた位相空間の点の数(= 重み)は、その巨視的状態の体積(volume)W です。
二つの独立した部分系が巨視的状態によって特徴付けられるとき、独立な部分系の巨視的状態の体積の積が系全体の体積になります。 乗法的性質は加法的性質ほど役には立たないので、位相空間の体積の対数である新しい属性を定義します。 この属性が巨視的状態のエントロピーで、ボルツマン(Bortzmann)の等式によって定義されます:
エントロピー = k log 体積 、 もしくはより簡潔に S = k log W 。 ただし k はボルツマン定数です。
k は正なので、エントロピーは微視的状態の「不確かさ」の尺度である体積と単調な関係にあります。
私たちはエントロピーを巨視的状態の確率ではなく位相空間における体積を用いて定義しましたが、これらの定義は同等なものです。 ここで、W0を定数として確率は p = W∕W0 なので、S = k log W∕W0 = k log W − k log W0 となり、違いは定数分だけになります。 私たちはエントロピーの絶対値ではなく変化に興味を持っているので、この定数の加算は重要にはなりません。
シャノン(Shannon)は情報を不確かさの減少(情報はエントロピーの減少)と定義し、情報をボルツマン定数の単位ではなくビットで量りました。 したがって、エントロピーと情報の1ビットの変化は、位相空間における体積を倍するか半分にするかに対応します。 情報とエントロピーは同じ物理現象です。 エントロピーは位相空間での不確かさを量る尺度で、巨視的状態から微視的状態を完全に決定するのに必要な追加的な情報の量です。 したがって、情報は負のエントロピーで、情報が増えればエントロピーは減ります。私たちはエントロピーをビットでも量るでしょう。
ボルツマン定数 k は、エントロピーの単位をエネルギーや温度と比較出来る単位へと変換します。 けれども、温度はアドホックな温度のスケールを用いるよりも、エネルギーを用いてより自然に定義することが出来ます。 そして、計算機科学では「エネルギー」はしばしば物理的なエネルギーとは無関係な抽象的な量として定義されるでしょう。
熱力学(Thermodynamics)にはmixing/ergodic(訳注: ergodicは「エルゴート的」だろうけどmixingは何? ergodic motion = 非周期運動?)な「運動」の概念が暗黙のうちにありますが、しかしエントロピーと情報は静的に定義することが出来ます。そのため、いかなる動的な変化も無い静的な状況設定にも情報やエントロピーは存在します。 したがって、情報とエントロピーの概念はより適切には(運動への要件を除いた)熱統計学(Thermostatistics)に属します。 例えば計算機科学においては、情報が格納されたデータの概念は、データが変化しないときでも役に立ちます。
古典的な粒子の力学では微分方程式は時間変数に関して可逆です。 したがって、全ての粒子のモーメントをあるタイミングで反転すれば、その系は最初の状態へと逆に発展するでしょう。 言い換えれば、古典力学の系は可逆で、したがって任意の時点で情報を保存するということです。
リウヴィルの定理の定理は可逆性と位相空間での体積について論じています。 古典力学によれば、単一の微視的状態の発展は一本の筋道で、時間が進む方向にも戻る方向にも分岐はありません。 リウヴィルの定理によれば、位相空間における微視的状態の集合のサイズ(すなわち体積)は、システムの発展の間変化しません。 もし、体積が変化するとすると幾つかの筋道は合流もしくは分岐することになってしまいます。 そのような分岐や合流は微視的可逆性に反するので、したがって体積は一定に保たれているはずです。
各巨視的状態には別々の微視的状態(の集合)が関連付けられているので、リウヴィルの定理によれば、最初の巨視的状態の体積は系の微視的可逆な発展の間、変化しません。 しかし、この体積の中身が系の発展に伴ってコンパクトであり続けるとか、連結であり続けるとかいった保障は何もありません。 実際、この体積の中身の最も短い記述は「ある微視的可逆な系をある特定の巨視的な初期状態からある時間だけ発展したもの」であることは、大いに有り得ることです。 例えば、微視的可逆な系は全てのより小さなチューリングマシンを対角化する可逆チューリング機械かもしれないのです。 したがって、リウヴィルの定理は「位相空間は圧縮できない」という主張に要約することが出来ます。 何故なら、微視的状態の「濃度」は時間にわたって変化しないためです。
(量子物理が真に微視的可逆である[Cramer86]か、そうでない[Penrose89]かは分かっていません。 しかし、もしそうでなくても、情報の中身を保存しないにしても、情報の総量は保存するはずです。 そのため、情報の創造と破壊は相互に強く結び付けられていなくてはなりません。 すなわち、リウヴィルの定理はより弱い「位相空間での体積は変化しない」という意味で成立するはずです。 量子暗号は、どんな観測も「波動関数を収縮させる」ため光子に保存された情報を全て取り出す事は出来ない[Bennett92]ということに基づいています。 この知識と無知の同時生産は、情報それ自体の不変性を示すのではないにしろ、宇宙の情報の総量の不変性を示すのかもしれません。)
自然熱力学の混乱の元は、状態と可逆という語の不適切な使い方の結果です。 熱力学の状態という語は巨視的状態を指していて、したがって多くの微視的状態を表しています。 そのため、計算機科学での意味での特定の「状態」(すなわち微視的な状態)を指しません。 自然熱力学は可逆という単語を、系が最初の微視的状態に戻る過程ではなく、最初の巨視的状態へ戻る過程に対して用います。 巨視的可逆性はリウヴィルの微視的可逆性の概念よりもかなり弱い概念です。 微視的可逆性は巨視的可逆性を含意しますが、その逆は成り立ちません。
カルノーの熱機関は(巨視的)「可逆」な過程として記述されます。 この過程では加熱・圧縮・膨張などが、系が常に「平衡状態」にあるよう十分ゆっくり行われるため、この過程は「可逆」です。 しかし、単純な思考実験によってカルノー機関が微視的可逆でないことを示すことが出来ます。対応する1対の膨張と圧縮のストロークを考えましょう。 実際の膨張は様々な時間と衝撃の一連の分子の衝突から成り、実際の圧縮は別の一連の衝突からなります。 微視的可逆な過程では、最初と最後の微視的状態が一致するだけでなく、タイミングと衝撃の大きさもすべて一致しなくてはなりません。 しかし、そのように一致するように整えるのは伝統的な巨視的過程では不可能です。
自然熱力学では巨視的可逆性は「エントロピーの保存」と同値で、さらにこれは位相空間での体積の保存に等しいです。 巨視的可逆性は保存された体積の中身が系の微視的可逆な発展によって関係することを要件としませんが、しかしその体積が等しいことだけを要件とします。 すなわち、巨視的可逆性は個々の微視的な発展の筋道が分岐したり合流することを禁止しませんが、それらの分岐や合流の集積された結果は総体積を保存します。 すなわち、「エントロピーの保存」は「情報の保存」を意味せず、位相空間での体積すなわち「エントロピーの総量の保存」だけを意味するのです。 シャノンの「情報」という用語はエントロピーの偽名であるので、したがって「以前の微視的状態を復元するのに必要なもの」という計算機科学における「情報」の意味を伝えるのに失敗しています。 (訳注: エントロピーが保存されても計算機科学の意味での情報は保存されないことがあるから、でいいのかな?)
微視的と巨視的の可逆性については議論しましたが、不可逆性については議論していませんでした。不可逆な系はリウヴィルの定理が成り立たない系です。 すなわち、情報は保存されず散逸します。 したがって、「散逸系(dissipative system)」[Prigogine84]という言葉の「散逸」はエネルギーではなく情報の散逸について言っています。 そのような系は通常エネルギーも同様に失いますが、不可逆な系を特徴付ける振る舞いをもたらすのは情報の散逸です。そのような特徴としては、例えば初期条件を忘れる「limit cycles」があります(訳注: limit cycle とその説明はどう訳すべき?)。
物理的な系は実際に微視的可逆であるかもしれませんが、ある程度の自由度を無視するのなら、ほとんどの手ごろな数学的モデルは不可逆になります。 そのような例として中性子のプロトン、電子、ニュートリノへの崩壊があります。 この反応は原理的には可逆ですが、逆の反応が起こるためには三つの粒子が同時に衝突しなくてはならず、これは非常に稀なことです。 また、ニュートリノが物体と相互作用するのは非常に稀なので、この逆反応は実質的には決して起こりません。 この反応は、非常に大きな質量やエネルギーを運ぶことなく、価値ある情報を運ぶニュートリノの能力を示しています。
複雑で混沌とした振る舞いをする「散逸」系へのとても大きな興味は、微視的不可逆な系が存在することを認めることを意味するのではありません。 そうではなく、単に巨視的非可逆なモデルは、最も細粒度な近似を除いた全てを扱う、優れた数学的モデルであることを認めるというだけのことです。
熱力学の第一法則は「エネルギーが保存される」ことを示しています。 しかし、「エネルギー」とは何でしょうか? 古典力学では微視的状態の二次関数で、位相空間における原点(何の「活動」もない点)から距離の計量であるものです。 しかし、エネルギーはいくつもの違った形に変換することが出来ます。 現代物理はエネルギーを時間に対して共役な変数とするので、エネルギーの保存は実質的にトートロジーになります(「エネルギーは時間にわたって保存される属性です」[3])。 このトートロジーを前提として、計算機科学者は時間にわたって保存される幾つもの抽象的な量の一つを系の「エネルギー」として選ぶことが出来ます。 もし、私たちが特定の対象や位置に結びつけることができる量を利用するならば、エネルギーについての物理的な直観は有効なままです。
系のエネルギーは部分系にわたって幾つもの異なる分布をすることが出来ます。 古典力学ではエネルギーは無限に分割可能なので、無限に多くの分布の仕方をすることが出来ます。 量子力学(と計算機科学では)「エネルギー」は量子化されるので、有限のエネルギーはたかだか可算通りの方法でしか分布出来ません。
系の総エネルギーは総サイズが一定である「ナップサック」のようなもので、総エネルギーがナップサックのサイズに等しいままならば、その中に様々なエネルギーのアイテムを配置することが出来ます。 熱力学の問題は通常、このナップサックを異なったエネルギーを持つこれらのアイテムで満たす方法の数え上げを伴います。 もし、ナップサックの大部分が一つか二つのアイテムに割り当てられているなら、小さなアイテムのために残っているエネルギーのスペースは少なく、したがってナップサックの満たし方の数は小さくなります。 同様に、もしナップサックの大部分が区別不可能な小さいアイテムに割り当てられている場合にも、ナップサックを満たす方法の数は限られます。 ナップサックを満たす方法の大部分は、多くの異なるサイズ(エネルギー)の多くの区別可能なアイテムを利用します。
ナップサック内の二つのアイテムが同じサイズ(エネルギー)を持つにも関わらず区別可能であることは縮退(degeneracy)です(この意味は通常期待されるのと反対です)。 縮退が無ければアイテムを区別する唯一の特徴はそのサイズ(エネルギー)です。 そして、非常に単純な量子系ではナップサックに入れるためのアイテムは基本的な量子エネルギーの整数倍だけです。
固定されたエネルギーと固定された個数の区別可能なアイテムを持つ単純な系を考えましょう。 すなわち、固定された個数の区別可能なスロットがあり、その個々は任意のサイズ(エネルギー)のアイテムを一個だけ収めます。 さらに、アイテムのサイズ(エネルギー)の和は、ナップサック全体のサイズ(エネルギー)に等しくなっています。 巨視的な数は二つ、すなわちスロットの数と総エネルギーの数しかないので、巨視的状態はそれらの数によって定義されます。 しかし、これらの条件を満たしている微視的状態は数多く存在します。巨視的状態の条件を満たすこれらの全ての微視的状態の中で「もっともありそう」な分布がマクスウェル・ボルツマン(MB)分布です。 マクスウェルはラグランジュ乗数とスターリング近似を単純に適用することでこの分布を発見しました。 MB分布では、あるスロットがあるエネルギーEを持つ確率は、β を分布の温度として exp(−βE) に比例します。 MB分布ではほとんどの粒子のエネルギーは小さく同じようなものです。 何故ならエネルギーを粒子の間に同じようなエネルギーで分配する方法は数多くあるためです。 もし、大きなエネルギーを持つ粒子が存在しないならば可能性の数は大きく減ります。少量の大きなエネルギーを許すMB分布は、最高の妥協を提供します。 (訳注: ここで言っている妥協というのは可能性の数に関する妥協でいいのかな)
MB分布では、スロットのエネルギーが高い確率は、「低い」温度よりも「高い」温度においての方が確率が大きいです。 さらに、分布全体におけるエネルギーの総量は「高い」温度のほうが高いです。 最後にエネルギー総量の増加はエネルギーの分布をより広くし、したがってエントロピーのキャパシティを増加させます。
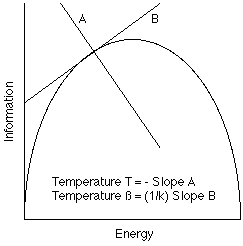
温度の現代的な抽象的な概念は、熱さについての我々の直観的 な概念とは本質的に異なります。現代的な統計熱力学は温度を、他の二つのマク ロな変数の微分から計算できる巨視的な変数として定義します。したがって、 Tを温度、Sをエントロピー、Eをエネルギーとすると、
1∕T = k β = dS∕dE, ただし k はボルツマン定数。
逆温度はエネルギーを一単位増やしたときのエントロピーの変化に比例します。エントロピーそれ自体は、位相空間の体積の対数に比例する ので、温度はエネルギーを一単位増やしたときの位相空間の体積の変化によっ ても定義出来ます。
1∕T = k β = dS∕dE = (d logW)∕dE = 1∕W × (dW∕dE)
単位量のエネルギーを追加したときのエントロピー(不確かさの分量)の変化が 小さな正の値であるならば、温度はとても高いです。もし、単位量のエネルギー を追加したときのエントロピーの変化が大きな正の値であるならば、温度はとて も低いです。古典的な系では、エネルギー容量(エネルギー準位の数)は無限で、 エネルギーの変化に伴うエントロピーの変化は常に正です。
しかし、系が持つことの出来るエネルギーに上限があって、高々有限の量のエネルギーしかシステムに与えられないのならば、エネルギーの追加に伴うエントロピーの変化が負になることがあります。 そのような系でエネルギー零の状態から始めて同じ量ずつエネルギーを追加していったときに何が起こるかを考えてみましょう、 最初、位相空間での体積は急速に拡大し、これは同時にエントロピーも増えている事を意味します。 もっとも、エントロピーは体積の対数なのでそれほどの速さではないですが。 エネルギーの各単位あたりのエントロピーの大きな増加は低い温度に特有です。 しかし、追加的なエネルギーが追加されていくと、エネルギーの同量の追加に対するエントロピーの増加はますますゆっくりになります。 この状況は高い温度に特有です。 そして、系の最大のエネルギーに上限が存在するのですが、最大のエネルギーに達するよりもずっと前にエントロピーの増加は横ばいになります。 この状況は無限大の温度に特有です。 もし、この点を超えてエネルギーを増加させるとエントロピーは減少を始めます! これは系のエネルギー収容力が飽和していて、エネルギーを追加する自由度がますます少なくなるためです。 この状況は負の温度に特有で、負の温度は実際には「無限大よりも熱い」温度です。 最後に、系が可能な最大のエネルギーに達したとき、エントロピーはしばしばゼロに落ちます。 何故ならば、系が最大のエネルギーを持つ方法はしばしばただ一つしか存在しないためです。
ケルビンの絶対温度 T はエントロピーが最大値に達する際に不連続になるので、現代の物理学者は代わりに逆温度 β=1∕kT を使うようになりました(物理的な単位はエネルギーの逆です)。「絶対零度」は β=+∞ を意味し、正常な温度は β>0 を意味し、無限大の温度は β=0 を意味し、異常な(「無限大よりも熱い」)温度は β<0 を意味することに注意しましょ う。

まとめると、系の温度とはエネルギーの変化に対する情報保存容量の変化を指しています。すなわち、 1∕T ∼ dInfo∕dEnergy となります。
ラプラス(Laplace)とフーリエ(Fourier)の時代には熱についての熱素(caloric)理論が流行していました。 この理論では熱は流体(fluid)であり、水が高いところから低いところへ流れるように、より熱い物体からより冷たい物体に流れるものでした。 熱容量とか熱流といった概念は、熱素流体(caloricfluid)の概念から生まれました。
エネルギーの概念の開発により物理学者は熱がエネルギーを含むことを知りましたが、しかし話はこれで終わりではありませんでした。 何故なら、高温にある熱エネルギーは同量の低温のエネルギーよりも価値がありましたし、力学的な「仕事」はどんな種類の熱エネルギーよりも価値があったからです。 クラウジウス(Clausius)は、エネルギーと同様に物体に出入りする「エントロピー」の概念を開発しました。 ボルツマンはこのエントロピーが単に位相空間の体積の対数であることを示し、ハートレー(Hartley)とシャノンはこのエントロピーを情報に関連付けました。 熱流はしたがって二つの独立したもの、エネルギー及び情報の流れを伴います。
温度の抽象的な概念は、系が持つエネルギー量の変化に対する情報記憶容量の段階的な変化の比率を指しています。 「高い」温度の場合には、同じビット数の情報を保存するのに、「低い」温度の場合よりもより多くのエネルギーを追加する必要があるということです。 別の言い方をするなら、「高温」の情報源(source)は、「低温」の情報源に比べて、単位量のエネルギーにより少ない情報しか施すことが出来ません。 さらに別の言い方をするなら、ある人にとっての情報は別の人にとってのノイズなので、「高温」のエネルギー源は「低温」のエネルギー源よりも騒々しくない、という言い方も出来ます。
カルノー(Carnot)は熱機関の性質、そして「熱」と「温度」の意味を説明する ために熱力学を発明しました。クラウジウス(Clausius)はそれからカルノーの モデルを定量化して、熱源と冷却装置の間で動く熱機関の最大効率を、熱 源と冷却装置の絶対温度の比を用いて表しました。
カルノーの熱機関の効率性の理論は、リウヴィルの定理と温度の(位相空間の体積と情報を用いた)定義を利用することで、より単純に説明することが出来ます。 二つの大きな「熱」源があり、それぞれの温度がTHとTLだとします。 温度の定義により、1∕THだけの情報=ノイズを高温の熱源から受け入れることにより、この熱源から単位量のエネルギーを得ることが出来ます。 同様に、TLだけのエネルギーを低温の熱源へ排出することで、単位量の情報=ノイズをこの熱源へ排出することが出来ます。 したがって、完全なサイクルは、単位量のエネルギーと1∕THの情報=ノイズを高温の熱源から受け入れ、続いてTL×(1∕TH)だけのエネルギーと1∕THだけの情報=ノイズを排出します。 等量(1∕TH)の情報=ノイズを受け入れ排出するので、熱機関内の情報の総量は一定に保たれます。過剰なエネルギー 1−(TL∕TH) が今「仕事」、すなわち情報やノイズ無しのエネルギーとして利用できます。 したがって、高温のエネルギーに対する行われた仕事という意味での効率は、(TH−TL)∕TH = (ΔT)∕TH となります。 私たちはTH>TLは要求しません。もし TH<TL であれば仕事は負になり、冷却装置になります。
「仕事」の情報収容力がゼロであることに注意してください。 そのため、追加的なエネルギーの追加はエントロピーを変化さまず、したがって「仕事」の「温度」は無限大です。 この定義は第二法則の通常の形式化が「エネルギーは高温の物体からから低温の物体へ流れる傾向がある」ことを述べているのと整合的です。 例えばコーヒーは沢山かき混ぜることで加熱することが出来ます。 (なお、そうするとコーヒーは水分子とスプーンの間のあらゆる衝突を記憶します。)
熱機関の効率性についてのカルノーの理論は温度の定義と微視的可逆性から直接導かれます。 カルノー自身は微視的可逆性ではなく巨視的可逆性を使っていたにも関わらず、効率に関する結果は同じように導くことが出来ます。 しかし、そのような熱機関は現実世界に存在するかもしれないし、存在しないかもしれません。 可逆な熱機関の存在を保証するためには、リウヴィルの定理を使う必要があります。
温度の通常の定義は暗黙のうちに物体が「熱平衡状態」にあることを仮定しています。すなわち、物体のどんな部分も他の部分と同じ温度であるということです。 このときには、あらゆる自由度が同じ平均のエネルギーを持つことになるので、エネルギーについての「エネルギー等分配則(equipartition theorem)」は、トートロジーになります。 ここで、もしエネルギー等分配則が成り立たないとすると、つまりある自由度のエネルギーは他のよりも少ないとすると、どうなるか考えてみましょう。 しかし、「自由度」の定義からして、各自由度はあらゆる他の自由度同じだけの情報を収容量を持っています。 より低いエネルギーの自由度の温度は低いことになり、平衡の定義に反することになります。
エネルギーと情報がある系から他へと流れる能力は、その結びつきに依存します。 強い結びつきの元では二つの系はエネルギーと情報を容易に交換し、おそらくは急速に平衡状態へ達します。 弱い結びつきの元でも二つの系はいつかは平衡に達することが出来ますが、それまでには非常に長い時間がかかるかもしれません。
弱く結びついた系の例としては、コンピュータのCPUチップとヒートシンクがあります。 計算そのもののために使われる僅かな自由度は、ヒートシンクに絶えず存在する膨大な量のランダムな情報から、かなりうまく隔離されていなければなりません。 チップの設計が非常に貧弱でない限り、通常の状況下では、チップのワイヤとゲート上で信号を伝える自由度は周囲の環境とは熱平衡状態にはありません。 これは多くのエネルギーが転送される一方で、相対的にわずかな情報しか転送されないためです。
弱く結びついた他の系として磁界中の数多くの核の量子スピン状態の系があります。 磁界の反転後、核が再び平衡状態に達するには多少の時間があかるかも知れませんが、それまでの時間それらの核のスピンの「温度」は無限大よりも熱く、すなわち負です[Marvan66]。(訳注: この例良くわからないよ……)
統計熱力学の幾つかの概念を実際のガベージコレクションされるヒープに適用するためには、まず系の「エネルギー」として機能するような保存量を見つけなくてはなりません。
管理下にあるストレージ上の場所の総数は、明らかにそのような量です。
なぜなら、通常の状況なら(すなわちそのヒープが爆弾を制御するアプリケーションの一部でもないなら)、そのようなストレージ上の場所は決して作られたり破棄されたりしないためです。
追加的なストレージをシステムから(例えばUnixの「brk」によって)獲得するストレージマネージャは、追加的なエネルギーを獲得できる物理的な系と類似した方法で扱えます。
ストレージマネージャによって保存される別の重要な量は、「生きている」オブジェクトに必要なストレージの容量です。でなければ、ストレージマネージャはアプリケーションに干渉してしまいます。
ストレージマネージャには「生きている」オブジェクトに格納されたアプリケーションの情報の大部分を見ることは許されないので、これらのデータはヒープに保存されたストレージマネージャの情報としては扱いません。 しかし、オブジェクトのサイズや位置、ひょっとしたら他のオブジェクトへのポインタなどは、ストレージマネージャに関する情報と考えることが出来るでしょう。 したがって、ストレージマネージャの管理下にある自由度は、アプリケーションの管理下にある自由度とはゆるく結びついているだけで、そのため異なった「温度」を持つことが出来ます。
例えば、ポインタの存在しないクヌース流のストレージマネージャ[Knuth73]では、関連する情報はストレージブロックのサイズ、場所、live/freeの状態だけです。 relocationを行わないLispのconsセルのガベージコレクタでは、関連する情報はポインタと「リストとアトムの区別の情報」を含むでしょうし、位置(無関係)とサイズ(定数)の情報は含まないでしょう。 copying collector の場合にはサイズとポインタの情報が関係するでしょうし、位置の情報は関係するかもしれないし関係しないかもしれません。 最も単純な状況は、固定サイズのブロックで、relocationが存在せず、ポインタも存在しないようなストレージマネージャです。そのようなシステムでの情報には全ブロックについてのlive/freeの状態のビットだけが含まれるでしょう。
ガベージコレクションされない(クヌース流の)ヒープでは、ヒープのエントロピーは主にヒープの断片化です。 ガベージコレクションされるヒープでは、ヒープのエントロピーは断片化および生存情報の喪失に結びついています。 しかし、ガベージコレクションされるヒープの場合には、モデル化されているのが誰の知識であるかについて、とても注意深くならなくてはいけません。 というのも、ガベージコレクタはいつでも(あるコストで)生きているオブジェクトを生きていないオブジェクトから推定区別可能だからです。 いつものように、ヒープのエントロピーはある巨視的変数(例えば、生きているオブジェクトの数、生きているオブジェクトのサイズの合計、なと)と整合的な微視的状態の体積と単調の関係にあります。
ガベージコレクションされるシステムでのmutator(アプリケーションのコード)はallocationと変更の活動によって情報/エントロピーをヒープに加えます。 そして、allocationレートの変化に対する情報の変化の比が、mutatorの「温度」として用いられるでしょう。
等しいサイズの場所からなる単純なヒープの温度を考えましょう。 単位量の「エネルギー」すなわちストレージ上の生きている場所を一つ追加したときの、ヒープの情報の変化が温度になります。 まず、(全てがフリーブロックである)空のヒープに生きている場所を一つ生きている場所を追加したとしましょう。 この単純なケースでの情報の総量は、ストレージの N+1 個の位置のうちのどれがその生きているオブジェクトであるかを特定するのに必要な情報で、すなわちlog(N+1)ビットです。 一方、N∕2 個のストレージ位置が生きているときには、ヒープのエントロピーは極大になり、温度も無限大になります。 さらに、生きているストレージ位置を増やすと、段々エントロピーが減少し、負の伝統的な温度(「無限大よりも熱い」)へと進みます。 ヒープのfullでは伝統的温度のマイナス零度に達します。 もし、伝統的温度Tの代わりに逆温度βを使うなら、 これは β=+∞ から β=0 を経て β=−∞ に至る滑らかな変化になります。
古典的な Lisp 1.5 のシステムにおけるフリーリスト(free storage list)のエントロピーは、無限のフリーリストを仮定すればゼロです[4]。 そして、情報を追加できないので、伝統的温度は無限大になります(すなわち、熱力学的な仕事です)。 異なったサイズのブロックを持つシステムのためのフリーリストは、ブロックのサイズと位置に関する相応の情報を持ちます。 同様に、リファレンスカウントのデクリメントを遅延するシステムにおいては、 free stack (訳注: 良い訳はないだろうか?)上の non‐decomposed objects (訳注: 自身のカウンタは0になったが参照先のカウンタをまだデクリメントしていないオブジェクトのことだと思う。どう訳するのが良いかな?)もまた相応の情報を持っていて、これはストレージが再利用される前に捨て去り忘れなくてはなりません。
Compactingガベージコレクタは幾つかの種類の情報を捨てます。 ほとんどの copying algorithm は冪等(idempotent)で、つまりGCを二回続けて実行した結果のメモリ配置は一回だけしか実行しなかった場合と同じになります。 このようなGCは、GC結果では有り得ないメモリ配置をGC結果であるメモリ配置へと変換するので、正規化の作業を行っていることになります。 Copying GC がガベージコレクションを行う際には、生きているセルをアドレス空間の連続した部分へとコンパクト化することによって、ゴミが「絞り取られる」はずです。その際に、ゴミが格納されていた隙間の位置とサイズの情報は破棄されます。 「address order preserving」コピー[Fisher74]は、ゴミを絞り取ることで生きているオブジェクトたちをコンパクト化しますが、その際に生きているオブジェクトのメモリ上の順序(たいていオブジェクトの生まれた順序と同じ)は保ちます。 順序を保存しないコピーには、年齢ではなく到達可能性に基づいて深さ優先(スタック)や幅優先(キュー)でトラバースを行うもの等があります。 この場合には、n を生きているオブジェクトの数として、約 n×logn ビットの順序情報を更に除去します。この情報は参照の局所性を保つのに重要かもしれません[Courts88]。
Copying GC の1サイクルの終わりには、GCに関するエントロピーは極小の状態にあります。 何故ならGCの活動それ自体が、どのアイテムがゴミであるかということについての不確実性を減少させ、またオブジェクトの場所を標準化(canonicalize)するためです。 しかし、mutatorがこの沢山の情報(訳注: エントロピーが極小ということは「負のエントロピー」という意味での情報は極大になっている)を拭い去るにはほんの数命令しかかかりません。 GCの終了直後には、生きているオブジェクトが一つ死ぬと、どれが死んだかを特定するための logn ビットが必要になります。 その後 n∕2 個の生きているオブジェクトが死んだ後には、どのオブジェクトが生きているか特定するために約 n ビット必要になります。 これは言い換えると死んだオブジェクト1つにつき2ビットの計算になります。 logn ビットから始まって n ビットに増えているので、温度はより高くなっています。 別の言い方をすると、一つのGCサイクルの終わりには温度は最低の点(願わくばゼロ)にありますが、アプリケーションプログラムの活動の間急速に上昇します。 これはすなわちガベージコレクタは冷却装置であるということです。
ガベージコレクタによって行われる計算的仕事(computational work)は、ヒープから絞り出す情報の量によって測ることが出来ます。 ガベージコレクタは、ヒープについての質問をし、情報を含んだ答えを得ることによってだけ、情報を引き出すことが出来ます。 つまり、ヒープから1ビットの情報を引き出すには、ガベージコレクタがまだ答えを知らないような二択の質問をしなくてはなりません(すなわち、答えはその時点では半々の確率でなくてはなりません)。 ヒープから k ビットを取り出すには、少なくとも k 個の二択の質問がされなくてはなりません。 しかし、ガベージコレクタのプログラムの大部分の条件文は結果が等確率ではありません。 そのため、質問毎に得られる情報は1ビットよりも少なくなり、 k ビットを取り出すためには k 回より多く二択の質問をしなければなりません。 この計算的仕事の特徴づけは直列とか並列とかの特定の計算モデルからは独立していることに注意してください。 最も効率的なガベージコレクタは結果が本当に分からない「効率的」な質問をするでしょう(例えば分岐予測が役に立たないような)。 また、1ビットよりも多くの情報を生み出す質問をするでしょう(e.g., some sort of dispatch operation)(訳注: 1ビットよりも多くの情報を生み出すってどういうことだ?)。 この計算のモデルはキャッシュとパイプラインを持つプロセッサと整合的で、そのようなプロセッサでは時間は通常の予測可能な活動にではなくキャッシュミスとパイプラインバブルに比例します[5]。
Compacting GC は、前のGCの終了後に割り当てられたセルを、前のGCを生き延びたセルから簡単に隔離することが出来ます。 したがって、GCが次に呼ばれたときにはアドレス空間には、新しく割り当てられたセルと前のGCを生き延びたセルからなる二つの異なる連続した部分があります。 世代別ガベージコレクションの仮説はこの二つの部分(「世代」)が互いに熱平衡状態になく、一方は他方よりも高温であるということです。 これらの異なった温度を計算してみましょう。 ある世代の逆温度は、そこへ新しく生きているオブジェクトを加えたときのエントロピーの変化です。 古典的な温度は絶対零度(生きているオブジェクトは存在しない)で始まり、無限大(半分のオブジェクトが生きている)へと上昇し、それからマイナス無限大からマイナス絶対零度へと上昇します。 それと同時に逆温度βは+∞から0を経て−∞へと滑らかに変化します。 すなわち、逆温度βは回収可能なゴミの割合と単調な関係にあります。 このように各世代の温度を計算することが出来ます。 そして、熱力学の言葉を使って表現すると、世代別GCは最新の世代の温度は前の生き残った世代の温度よりも低いという仮説に拠っています。
世代別GCの仮説: 新しい世代の温度 < 生き残った世代の温度
この仮説をくだけた言葉で解釈してみましょう。 ある世代の温度はストレージのセルを回収するための情報の(限界)費用です。 そして、世代別GCの仮説は「新しい世代からセルを回収する限界費用は、生き残っている世代からセルを回収する限界費用よりも低い」ということを述べています。 ある世代をガベージコレクションする本当の費用は限界費用ではなく全ての回収されるセルの平均費用ですが、私たちはほとんどの回収されるセルは限界費用に近い費用を持ち、限界費用が平均費用のリーズナブルな見積もりであることを仮定します(訳注: そのような仮定が出来るのは何故?)。 もし、温度に大きな違いがあり、系が平衡状態からほど遠いのであれば、新しい世代からセルを回収する費用は、生き残っている世代からセルを回収する費用よりも低くなるでしょう。 平均費用は世代の大きさや他の要因に依存するので、限界費用は平均費用よりもロバストな指標です(訳注: 何故ロバストと言えるのか?)。
ガベージコレクタのような複雑なシステムのある種の性質を明らかにするために、統計熱力学の幾つかの概念をいかに使うことが出来るかを示してきました。 私たちは、マンデルブロ(Mandelbrot)による単語の出現度数分布と平衡エネルギー分布のアナロジー、およびマーゴラス(Margolus)による保守的論理(conservative logic)の熱力学に触発されました。
焼きなまし法(simulated annealing) [Kirkpatrick83] のテクニックは、温度の概念を反対の向きに利用します。 これはエネルギーのマクスウェル・ボルツマン分布を仮定し、大きなエネルギーを持つ自由度をゆっくりと締め出していく過程で最小のエネルギー準位を探します。 焼きなまし法には、本当に最小のエネルギーを見つけるかどうかの保障はありませんが、それは最小のエネルギーを見逃してしまうことを最小にしようとします。 温度が減るにつれ、エネルギーの追加毎に必要な「情報の変化」は大きくなります。 そして、ある時点でエネルギーの更なる減少は割りにあわなくなります。 (訳注: この説明はいまいち良くわからないな)
ガベージコレクションと焼きなまし法は共に「冷却」を行うので、ガベージコレクションには最適化の分野と交差する領域がまだ他にもあるかもしれません。 ひょっとしたら、GCでのコピー中に焼きなまし法を使う事で参照の局所性を最適化出来るといったことがあるかも知れません。